S. H. Cullinane
The relativity
problem in finite geometry.
Feb. 20, 1986.
This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them.
—
H. Weyl, The Classical Groups ,
Princeton Univ. Pr., 1946, p. 16
In finite geometry "points" are often defined as ordered n-tuples of a finite (i.e., Galois) field GF(q). What geometric structures ("frames of reference," in Weyl's terms) are coordinatized by such n-tuples? Weyl's use of "objectively" seems to mean that such structures should have certain objective— i.e., purely geometric— properties invariant under each S.
This note suggests such a frame of reference for the affine 4-space over GF(2), and a class of 322,560 equivalent coordinatizations of the frame.
The frame: A 4×4 array.
The invariant structure:
The following set of 15 partitions of the frame into two 8-sets.

A representative coordinatization:
0000
0001 0010 0011
0100 0101 0110 0111
1000 1001 1010 1011
1100 1101 1110 1111
The group: The group AGL(4,2) of 322,560 regular affine transformations of the ordered 4-tuples over GF(2).
S. H. Cullinane
The relativity problem in finite geometry.
Nov. 22, 2012.
This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them.
—
H. Weyl, The Classical Groups ,
Princeton Univ. Pr., 1946, p. 16
In finite geometry "points" are often defined as ordered n-tuples of a finite (i.e., Galois) field GF(q). What geometric structures ("frames of reference," in Weyl's terms) are coordinatized by such n-tuples? Weyl's use of "objectively" seems to mean that such structures should have certain objective— i.e., purely geometric— properties invariant under each S.
This note suggests such a frame of reference for the affine 4-space over GF(2), and a class of 322,560 equivalent coordinatizations of the frame.
The frame: An array of 16 congruent equilateral subtriangles that make up a larger equilateral triangle.
The invariant structure:
The following set of 15 partitions of the frame into two 8-sets.

A representative coordinatization:
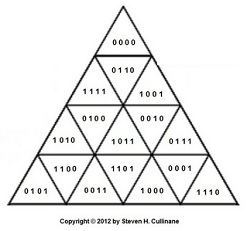
The group: The group AGL(4,2) of 322,560 regular affine transformations of the ordered 4-tuples over GF(2).