Steven H. Cullinane

Generating the Octad Generator

Expository note.  April 28, 1985.

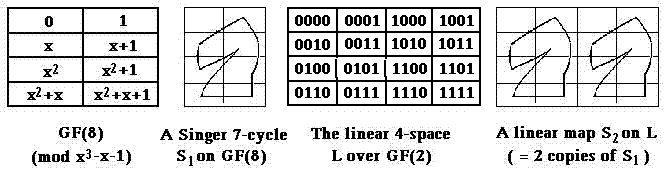
Apart from its use in studying the 759 octads of a Steiner system S(5,8,24) -- and hence the Mathieu group M_{24 --} the Curtis MOG nicely illustrates a natural correspondence C (Conwell [2], p. 72) between

(a)  the 35 partitions of an 8-set H (such as GF(8) above, or Conwell's 8 "heptads") into two 4-sets, and

(b)  the 35 partitions of L into four parallel affine planes.

Two of the H-partitions have a common refinement into 2-sets iff the same is true of the corresponding L-partitions.  (Cameron [1], p. 60).

Note that C is particularly natural in row 1, and that partitions 2-5 in each row have similar structures.

1. _{Cameron, P. J., Parallelisms of Complete Designs, Camb. U. Pr. 1976.}
2. _{Conwell, G. M., The 3-space PG(3,2) and its group, Ann. of Math. 11 (1910) 60-76.}
3. _{Curtis, R. T., A new combinatorial approach to M24, Math. Proc. Camb. Phil. Soc. 79 (1976) 25-42.}

For an image of the original 1985 typed note, click here.