Finite Geometry Notes   | Home | Site Map | Author |

Pilate Goes to Kindergarten  (April 2009, with update of February 2012)

"There is a pleasantly discursive treatment of Pontius Pilate's unanswered question 'What is truth?'."

-- H. S. M. Coxeter, 1987, introduction to Trudeau's The Non-Euclidean Revolution

Consider the following question in a paper cited by V.S. Varadarajan:

E. G. Beltrametti, "Can a finite geometry describe physical space-time?"

 (Universita degli studi di Perugia, Atti del convegno di geometria combinatoria e sue applicazioni, Perugia 1971, 57–62)

Simplifying:

"Can a finite geometry describe physical space?"

Simplifying further:

"Yes. Vide 'The Eightfold Cube.'"

Let G be the group of 1344 transformations of the 3-dimensional affine finite geometry over the 2-element field GF(2).

The eightfold cube illustrates one property of physical space-- namely, the invariance under G of the set of seven partitions illustrated with kindergarten blocks below.

These seven partitions are a model, in physical space, of the seven points of the 2-dimensional projective finite geometry over GF(2). The partitions (i.e., the projective points) are permuted by G, a group generated by physically natural permutations of the eight subcubes.

Froebel's 'Third Gift' to kindergarteners: the 2x2x2 cube

Update of February 17, 2012

Pregeometry and Finite Geometry

The February 2012 Scientific American  article "Is Space Digital?"
suggested a review of a notion that the theoretical physicist
John Archibald Wheeler called  pregeometry .

From a paper on that topic—

"… the idea that geometry should constitute
'the magic building material of the universe'
had to collapse on behalf of what Wheeler
has called pregeometry (see Misner et al. 1973,
pp. 1203-1212; Wheeler 1980), a somewhat
indefinite term which expresses “a combination
of hope and need, of philosophy and physics
and mathematics and logic” (Misner et al. 1973,
p. 1203)."

— Jacques Demaret, Michael Heller, and
Dominique Lambert, "Local and Global Properties
of the World," preprint of paper published in
Foundations of Science  2 (1): 137-176

Misner, C. W., Thorne, K. S. and Wheeler, J. A.
1973, Gravitation , W.H. Freeman and Company:
San Francisco.

Wheeler, J.A. 1980, "Pregeometry: Motivations
and Prospects," in: Quantum Theory and Gravitation ,
ed. A.R. Marlow, Academic Press: New York, pp. 1-11.

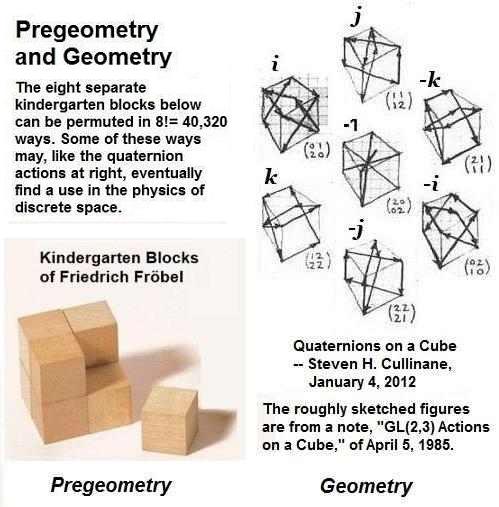
Some related material from pure mathematics—

IMAGE- Pregeometry (kindergarten blocks) and geometry (quaternions on a cube)

Click image for further details.

Page created on April 10, 2009 (Good Friday). Updated February 17, 2012.