A Four-Color Theorem:
Function Decomposition Over a Finite Field
by Steven H. Cullinane
The proof of the diamond theorem
involves the following elementary, but new and useful, result:
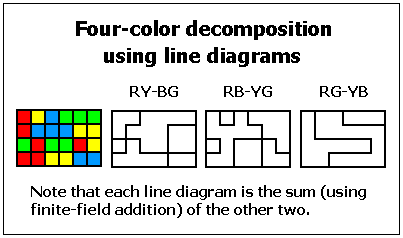
Every 4-coloring (i.e., every function into a 4-set) can be
expressed as a sum of three 2-colorings (into GF(4)).
(Or, equivalently, as a linear combination of three
2-colorings (into GF(2) as a subfield of GF(4))).
How this works:
Let m be a map into a 4-set.
Represent the elements of the 4-set by the elements {0, 1, a, b}
of the finite field GF(4), so that m becomes a map f into
this field.
Define f(x,y), where x, y are elements of GF(4),
as the map into GF(4) that has value 1 wherever f has
value x or y, and that has value 0 elsewhere. Then
f = 1f(a,b) + af(1,b) + bf(1,a)
A modest generalization of the decomposition theorem, and a problem
disguised as a query, are given by the 1982 research note below.

View original
1982 note.
The decomposition theorem's algebraic formulation above is useful for
showing, for instance, that certain four-colored graphic images can
form a ring under multiplication.
But in applying the decomposition theorem, we often are interested only
in
the partition lines separating regions colored by complementary
2-subsets of the 4-color
set.
Example:
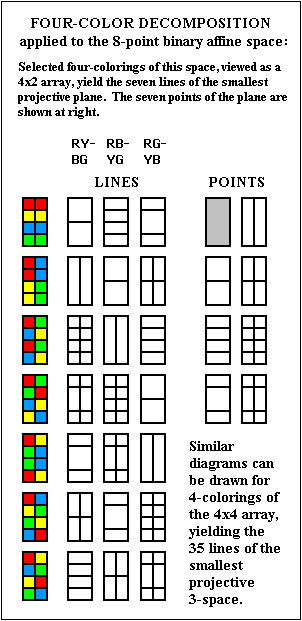
Example:
Example:
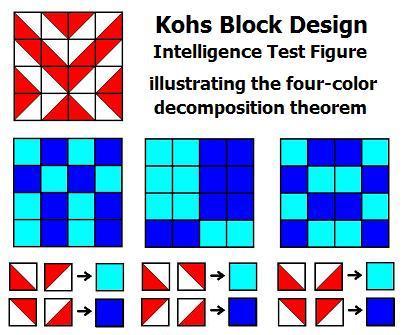
Kohs Block Design Test figure
illustrating the four-color decomposition theorem
|
Application of
Four-Color Decomposition:
The Diamond Theorem
We regard the four-diamond figure D below as a
4x4 array of two-color diagonally-divided square tiles.
Let
G be the group of 322,560 permutations of these 16 tiles generated by
arbitrarily mixing random permutations of rows and of columns with
random permutations of the four 2x2 quadrants.
THEOREM: Every G-image of D (as at right, below)
has some ordinary or color-interchange symmetry.
Example:
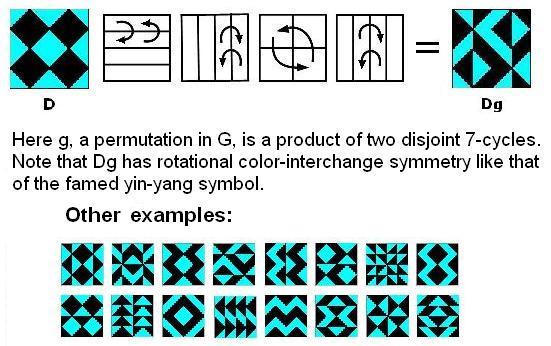
For an animated version, click here. |
For more on how the decomposition theorem
applies to the diamond theorem, click here.
Related material:
Orthogonal Latin
Squares as Skew Lines.
Page last maintained August 22, 2008; created Nov. 27,
2001.




