Inscapes
by Steven H. Cullinane
In finite geometry and combinatorics,
an inscape is a 4x4 array of square figures,
each figure picturing a subset of the overall 4x4 array:
an inscape is a 4x4 array of square figures,
each figure picturing a subset of the overall 4x4 array:

Inscapes provide a way of picturing
the following equivalent concepts:
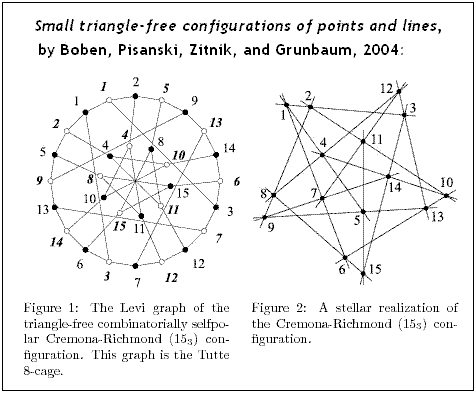
The 60 (= 15×4) Göpel tetrads in PG(3,2),
The generalized quadrangle GQ(2,2),
Tutte's 8-cage, and
the Cremona-Richmond 153 configuration (pdf):
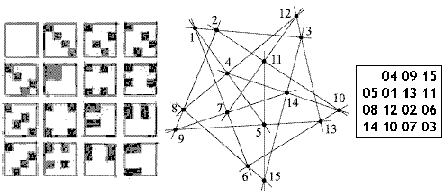
Diamond Theory
shows that this structure
can also be modeled by an
inscape:

The illustration below shows how the
points and lines of the inscape may
be identified with those of the
Cremona-Richmond configuration.
Related material on inscapes:
Rosenhain and Göpel Tetrads in PG(3,2)
The
2-Subsets of a 6-Set are the Points of a PG(3,2)
A
Symplectic Approach to the Miracle Octad Generator
Inscapes, Inscapes II, Inscapes III, Inscapes IV
Page created Jan. 19, 2006. Last modified March 26, 2013.