Diamond Theory by Steven H. Cullinane

Plato's Diamond

Motto of Plato's Academy

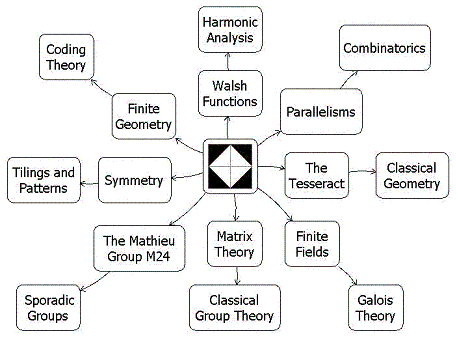
Symmetry is often described as invariance under a group of transformations. An unspoken assumption about symmetry in Euclidean 3-space is that the transformations involved are continuous.

Diamond theory rejects this assumption, and in so doing reveals that Euclidean symmetry may itself be invariant under rather interesting groups of noncontinuous (and asymmetric) transformations. (These might be called noncontinuous groups, as opposed to so-called discontinuous (or discrete) symmetry groups. See Weyl's Symmetry.)

For example, the affine group A on the 4-space over the 2-element field has a natural noncontinuous and asymmetric but symmetry-preserving action on the elements of a 4x4 array. (Details)

By embedding the 4x4 array in a 4x6 array, then embedding A in a supergroup that acts in a natural way on the larger array, one can, as R. T. Curtis discovered, construct the Mathieu group M₂₄ -- which is, according to J. H. Conway, the "most remarkable of all finite groups."

The proof that A preserves symmetry involves the following elementary, but useful and apparently new, result: Every 4-coloring (i.e., every map into a 4-set) can be expressed as a sum of three 2-colorings. It is conceivable that this result might have applications other than to diamond theory. (Details)

The proof that A preserves symmetry also yields some insight into orthogonality of Latin squares, at least in the 4x4 case. In this case, orthogonality turns out to be equivalent to skewness of lines in a finite projective 3-space. (Details)

Diamond theory provides simple ways to visualize

• "the simplest non-trivial model for harmonic analysis,"¹ the Walsh functions,
• "the smallest perfect universe,"² the finite projective space PG(3,2),
• the "distinguished geometry," "remarkable geometric individual," and "gem,"³ the finite projective plane PG(2,4),
• the "remarkable"⁴ outer automorphisms of S₆, and
• the structural equivalence of certain
  • factorizations³ of graphs,
  • parallelisms⁵ of partitions,
  • spreads⁶ of lines, and
  • sets of mutually orthogonal squares (i.e., n-orthogonal⁷ nxn matrices).

1.  F. Schipp et al., Walsh Series, 1990
2.  Burkard Polster, website
3.  A. Beutelspacher in the American Mathematical Monthly, January 1986
4.  P. J. Cameron and J. H. van Lint, Designs, Graphs, Codes, and their Links, 1991
5.  P. J. Cameron, Parallelisms of Complete Designs, 1976
6.  J. W. P. Hirschfeld, Finite Projective Spaces of Three Dimensions, 1985
7.  J. Denes and A. D. Keedwell, Latin Squares and their Applications, 1974

As a bonus, extending the action of A to a 4x4x4 array yields a simple way of generating the 1.3 trillion transformations natural to the 64 hexagrams of the I Ching. (Details)

Mathematics Subject Classification (MSC2000) - Primary: 20B25, Finite automorphism groups of algebraic, geometric, or combinatorial structures. Secondary: 05B25, Finite geometries; 51E20, Combinatorial structures in finite projective spaces.

---

To Shirley

On Euclid's Elements:
"In view of... admiration the Elements has consistently elicited over the years, and of the prestigious role it concomitantly maintained until the mid-19th century as scientific archetype, it is not surprising that we find in the history of philosophy a concept of truth sustained by the example of the Elements, whose influence in philosophy runs parallel to that of the Elements in science. This concept I will call the 'Diamond Theory' of truth."
-- Richard J. Trudeau in The Non-Euclidean Revolution, 1987

Introduction:

The image below shows the cover of a booklet I wrote in 1976. The booklet details the implications of what I call the "diamond theorem," after the diamond figure in Plato's Meno dialogue. This website, which updates the booklet, is written for mathematicians and college students of mathematics. For a less technical treatment of philosophical and literary matters related to the diamond theorem, see The Diamond Theory of Truth.

For some historical background to the diamond theorem, see

For material related to the diamond theorem, see the site map.

For some background on the philosophy of mathematics in general, see

The Non-Euclidean Revolution.
This 1987 book by Richard J. Trudeau, with a brief introduction by H. S. M. Coxeter, traces in the recent history of geometry the conflict between what Trudeau calls the "Diamond Theory of truth" and the "Story Theory of truth" -- known to more traditional philosophers as "realism" and "nominalism."

For more on Trudeau's version of diamond theory, see this site's companion website, The Diamond Theory of Truth.

For more on the story theory, consider the following quotation:

"The moral of my story is: Read Euclid and ask questions. Then teach a course on Euclid and later developments arising out of these questions."

The quotation is from Robin Hartshorne, the author of Algebraic Geometry, in "Teaching Geometry According to Euclid," Notices of the American Mathematical Society, April 2000.

---

Diamond Theory

Plato tells how Socrates helped Meno's slave boy "remember" the geometry of a diamond. Twenty-four centuries later, this geometry has a new theorem.

The Diamond Theorem: Inscribe a white diamond in a black square. Split the resulting figure along its vertical and horizontal midlines into four quadrants so that each quadrant is a square divided by one of its diagonals into a black half and a white half. Call the resulting figure D. D Let G be the group of 24 transformations of D obtained by randomly permuting (without rotating) the four quadrants of D. Let S4 denote the symmetric group acting on four elements. Then (1) Every G-image of D has some ordinary or color-interchange symmetry (see below), (2) G is an affine group generated by S4 actions on parts of D, and (3) Results (1) and (2) generalize, through intermediate stages, to symmetry invariance under a group of approximately 1.3 trillion transformations generated by S4 actions on parts of a 4x4x4 cube.

The 2x2 case In the 2x2 case, D is a one-diamond figure (top left, below) and G is a group of 24 permutations generated by random permutations of the four 1x1 quadrants. Every G-image of D (as below) has some ordinary or color-interchange symmetry.

Example of the 4x4 case In the 4x4 case, D is a four-diamond figure (left, below) and G is a group of 322,560 permutations generated by arbitrarily mixing random permutations of rows and of columns with random permutations of the four 2x2 quadrants. Every G-image of D (as at right, below) has some ordinary or color-interchange symmetry.
D	Let e denote transposition of the first two rows, f denote transposition of the last two columns, g denote transposition of the top left and bottom right quadrants, and h denote transposition of the middle two columns. Then Defgh is as at right. Note that Defgh has rotational color-interchange symmetry like that of the famed yin-yang symbol.	Defgh
Remarks on the 4x4 case: G is isomorphic to the affine group A on the linear 4-space over GF(2). The 35 structures of the 840 = 35 x 24 G-images of D are isomorphic to the 35 lines in the 3-dimensional projective space over GF(2). Orthogonality of structures corresponds to skewness of lines. We can define sums and products so that the G-images of D generate an ideal (1024 patterns characterized by all horizontal or vertical "cuts" being uninterrupted) of a ring of 4096 symmetric patterns. There is an infinite family of such "diamond" rings, isomorphic to rings of matrices over GF(4). For a movable JavaScript version of these 4x4 patterns, see The Diamond 16 Puzzle.

The statement of the theorem may be clarified by a research announcement written in 1978 that illustrates the above 4x4 example in reverse... Research Announcement, 1978 (pdf).

Illustrations of half-square patterns:

For an artist's rendering of some patterns generated as described in the diamond theorem (and many not so generated), see the following new (September 11, 2000) website: Tiling, by Mike Lyon.

For more illustrations and a sketch of the proof, see the following

Diamond Theory Research Notes

Hartshorne's principle: "Whenever one approaches a subject from two different directions, there is bound to be an interesting theorem expressing their relation." - Robin Hartshorne, AMS Notices, April 2000, p. 464.

( 1) Diamond theory cover page

From the author's 1976 booklet. See The Diamond Theory of Truth for the meaning of the cover illustration.

( 2) The relativity problem in finite geometry

"This is the relativity problem: to fix objectively a class of equivalent coordinatizations and to ascertain the group of transformations S mediating between them."
-- Hermann Weyl, The Classical Groups
For an application to analysis, see Symmetry of Walsh Functions.

( 3) Orthogonality of Latin squares viewed as skewness of lines

Structural diagrams of 4x4 arrays play the role of lines in PG(3,2). Orthogonality of arrays corresponds to skewness of lines.

( 3.1) Map systems

The algebra underlying note (3): Every 4-coloring can be expressed, using GF(4), as a linear combination of three 2-colorings. This elementary, but apparently new, result may have applications other than to diamond theory.

( 4) Diamonds and whirls

Block designs of a different sort -- graphic figures on cubes. See also the University of Exeter page on the octahedral group O.

( 5) Affine groups on small binary spaces

Six ways to slice a cube, and the resulting affine groups.
For details, see the author's 1984 paper Binary Coordinate Systems.

( 6) An invariance of symmetry

The diamond theorem on a 4x4x4 cube, and a sketch of the proof.

( 7) Generating the octad generator

The Miracle Octad Generator (MOG) of R. T. Curtis -- A correspondence between the 35 partitions of an 8-set into two 4-sets and the 35 lines of PG(3,2).
For more on the MOG, see, for instance, the preprint by Marston Conder and John McKay, "Markings of the Golay Code" -- either the author's PostScript version or the cached version. Other details on the Miracle Octad Generator are given in the reference file highlighted in yellow below.

( 8) The 2-subsets of a 6-set are the points of a PG(3,2)

Beutelspacher's model of the 15 points of PG(3,2) compared with a 15-line complex in PG(3,2).

( 9) Twenty-one projective partitions

The author's model of the 21-point projective plane PG(2,4).
For a general method of constructing such models, see Modeling PG(2,4).

(10) Inscapes

A new combinatorial concept that illustrates symplectic polarities in PG(3,2).

(11) Inscapes II

The concept in note (10) is generalized.

(12) Inscapes III

An excellent source of exercises related to note (12) is Introduction to the Theory of Groups of Finite Order, by Robert D. Carmichael (1937), reprinted by Dover Books, 1956. See especially
pp. 42-43, ex. 30 and 31;
p. 73, ex. 32;
p. 165, ex. 20;
p. 304, ex. 3;
pp. 320-321, ex. 7-12;
pp. 336-337, ex. 4-7, 9, 10;
p. 353, ex. 5;
p. 392, ex. 6, part (3);
p. 437, ex. 14-17;
p. 439, ex. 11-12;
pp. 440-441, ex. 20, 21.
These exercises in Carmichael have a simplicity and clarity lacking in many more recent works on finite mathematics.
See also "Generalized Steiner Systems of Type 3-(v,{4,6},1)," by E. F. Assmus, Jr., and J. E. Novillo Sardi, in Finite Geometries and Designs, edited by P. J. Cameron, J. W. P. Hirschfeld, and D. R. Hughes, Cambridge University Press, 1981.

(13) Inscapes IV

An outer automorphism that is literally outer.

(14) Portrait of O

A table of the octahedral group O using the 24 patterns from the 2x2 case of the diamond theorem.

(15) Study of O

A different way of looking at the octahedral group, using cubes that illustrate the 2x2x2 case of the diamond theorem.

(16) Symmetry invariance under M₁₂

A generalization of the two-color plane patterns, made up of all-black and all-white squares, that underlie plane patterns, made up of two-color diagonally-divided squares, of diamond theory.

Other research notes:

The above notes are directly related to the diamond theorem. For 23 other research notes less directly related to, but inspired (for the most part) by the theorem, see Miscellaneous Research Notes.

---

Plato, Pythagoras, and the diamond figure:

Plato's Diamond in the Meno
Plato as a precursor of Gerard Manley Hopkins's "immortal diamond." An illustration shows the prototype of the figure D discussed above.

Plato's Diamond Revisited
Ivars Peterson's Nov. 27, 2000 column "Square of the Hypotenuse" which discusses the diamond figure as used by Pythagoras (perhaps) and Plato. Other references to the use of Plato's diamond in the proof of the Pythagorean theorem:

Huxley --

"... and he proceeded to prove the theorem of Pythagoras -- not in Euclid's way, but by the simpler and more satisfying method which was, in all probability, employed by Pythagoras himself....
'You see,' he said, 'it seemed to me so beautiful....'
I nodded. 'Yes, it's very beautiful,' I said -- 'it's very beautiful indeed.'"
-- Aldous Huxley, "Young Archimedes," in Collected Short Stories, Harper, 1957, pp. 246 - 247

Heath --

Sir Thomas L. Heath, in his commentary on Euclid I.47, asks how Pythagoreans discovered the Pythagorean theorem and the irrationality of the diagonal of a unit square. His answer? Plato's diamond.
(See Heath, Sir Thomas Little (1861-1940),
The thirteen books of Euclid's Elements translated from the text of Heiberg with introduction and commentary. Three volumes. University Press, Cambridge, 1908. Second edition: University Press, Cambridge, 1925. Reprint: Dover Publ., New York, 1956. Reviewed: Isis 10 (1928),60-62.)

Other sites on the alleged "diamond" proof of Pythagoras --

Colorful diagrams at Cut-the-Knot

Illustrated legend of the diamond proof

Babylonian version of the diamond proof

---

Keywords to help place the diamond theorem in the proper mathematical context:

"We may say, roughly, that a mathematical idea is 'significant' if it can be connected, in a natural and illuminating way, with a large complex of other mathematical ideas."
- G. H. Hardy, A Mathematician's Apology (1940), Cambridge University Press, reprinted 1969, page 89

affine geometry, affine planes, affine spaces, automorphisms, binary codes, block designs, classical groups, codes, coding theory, collineations, combinatorial, combinatorics, conjugacy classes, the Conwell correspondence, correlations, Cullinane, R. T. Curtis, design theory, the diamond theorem, diamond theory, duads, duality, error correcting codes, exceptional groups, finite fields, finite geometry, finite groups, finite rings, Galois fields, generalized quadrangles, generators, geometry, GF(2), GF(4), the (24,12) Golay code, group actions, group theory, Hadamard matrices, hypercube, hyperplanes, hyperspace, incidence structures, invariance, Karnaugh maps, Kirkman's schoolgirls problem, Latin squares, Leech lattice, linear groups, linear spaces, linear transformations, Mathieu groups, matrix theory, Meno, Miracle Octad Generator, MOG, multiply transitive groups, octads, the octahedral group, orthogonal arrays, outer automorphisms, parallelisms, partial geometries, permutation groups, PG(3,2), Plato, Platonic, polarities, Polya-Burnside theorem, projective geometry, projective planes, projective spaces, projectivities, Reed-Muller codes, the relativity problem, Singer cycle, skew lines, Socrates, sporadic simple groups, Steiner systems, Sylvester, symmetric, symmetry, symplectic, synthemes, synthematic, tesseract, transvections, Walsh functions, Witt designs

Search engine for use with the above keywords:

Other search engines:

Google Directory of Mathematics Search Engines

Sites on combinatorics generally:

The Combinatorics Net
The Open Directory list of combinatorics sites
U. of London Permutation Groups Resources
U. of London Design Resources on the Web

---

Diamond Theory Bibliography

---

"It is a good light, then, for those
That know the ultimate Plato,
Tranquillizing with this jewel
The torments of confusion."
- Wallace Stevens,
Collected Poetry and Prose, page 21,
The Library of America, 1997

Ordering information for Wallace Stevens book

---

Page updated July 17, 2004, and again on May 25, 2006. Created June 21, 2000.

Copyright © 2001 by Steven H. Cullinane. All rights reserved.