Finite Geometry and the
16 Boolean Connectives
Abstract: The phrase "algebra of logic" is commonly used to describe the classic work of Boole and others. The phrase "geometry of logic" is less common; this note supplies some background on what it might mean.
It is well known that the set of 16 connectives ("and," "or," etc.) of two-variable Boolean logic and the set of 16 subsets of an four-element set (a 4-set) have the same structure-- a Boolean lattice. It is also well known that the group of Boolean-lattice automorphisms, or symmetries, of the 16 connectives is isomorphic to the group of 24 permutations of the 4-set. Nevertheless, some authors* have proposed additional automorphisms of the 16 connectives, based on symmetries of geometric figures (such as a Hasse diagram of the Boolean lattice) labeled by the connectives. Such proposed automorphisms may be viewed in a larger context-- that of the 322,560 automorphisms of the four-dimensional affine space A over the two-element Galois field GF(2).
The phrase "geometry of
logic" has been used by,
among others, David Miller of the department of philosophy at the
University of
Warwick. The following is from a talk by Miller:

Figure 1
Miller's "geometry of logic" is based on a pseudometric space. This note discusses a "geometry of logic" that differs from Miller's but is related to one of Miller's illustrations. Figure 1, Miller's picture of a Hasse diagram of a Boolean lattice, may also be viewed as a tesseract (4-dimensional hypercube) whose vertices represent the 16 traditional "binary connectives" (logical operations on two variables) of basic logic. The tesseract's 16 vertices may also, as in Figure 2, below, be regarded as representing either the 16 subsets of a 4-set or the 16 elements of the affine 4-space A over the two-element Galois field GF(2).
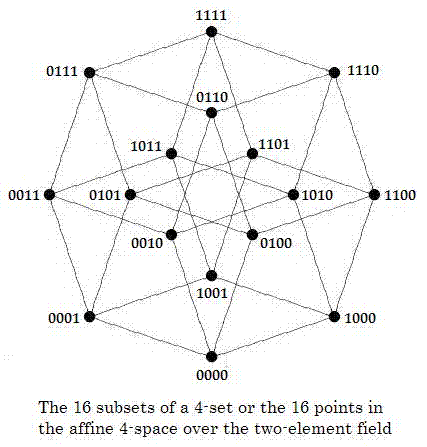
Figure 2
If interpreted as a Boolean-lattice diagram, this abstract structure has a group of automorphisms (one-to-one self-mappings preserving the partial ordering) of order 24, corresponding to the group of all permutations of an underlying 4-set.
If interpreted as a tesseract, the abstract structure has a group of automorphisms (one-to-one self-mappings preserving adjacency) of order 384.
The tesseract interpretation suggests a "geometry of logic" different from Miller's-- the geometry of the 4x4 square. Such a square, if interpreted as an adjacency structure (on a torus, i.e., with each cell on an edge of the array adjacent to the corresponding cell on the opposite edge), also has a group of 384 automorphisms-- essentially the same as those of the tesseract, since there is an adjacency-preserving isomophism of the tesseract's 16 vertices with the array's 16 unit cells. (See this site's discussion of a 1937 problem of R. D. Carmichael.)
As we applied labels to the tesseract, we can also apply labels to the 4x4 square. The 16 binary-connective labels of Figure 1-- redrawn as Venn diagrams-- and the 16 digital labels of Figure 2 can be applied to the 16 unit cells of a 4x4 square as in Figure 3 below.
The 4x4 array, can, like the tesseract, be viewed in various ways. If interpreted as a rigid geometric figure, the array has as automorphisms the group of 8 symmetries of the square. If interpreted as an adjacency structure, the array has, as noted above, a group of 384 automorphisms. If we do not require that an automorphism (or symmetry) of the array preserve adjacency of unit cells, the array may be viewed as having a much larger group of symmetries: 322,560. This is the order of the full affine group acting on the 16 digital labels, when these labels are regarded as names of the 16 points of the affine 4-space A over the two-element Galois field GF(2). (See "Geometry of the 4x4 Square.") For a purely geometric way to generate the affine group, without any reference to the digital labels (i.e., coordinates), see the kaleidoscope puzzle.
This affine group includes the previously mentioned groups of orders 8, 24, and 384 as subgroups.
Figure 3 below allows us to compare some authors' suggestions* for interesting permutations of the 16 binary connectives (here represented by Venn diagrams) with permutations acting, as in "Geometry of the 4x4 Square," on the 16 affine 4-space points (here represented by digital labels). A table by Donald E. Knuth is used to translate the Venn diagrams into the standard non-digital notations for the connectives.
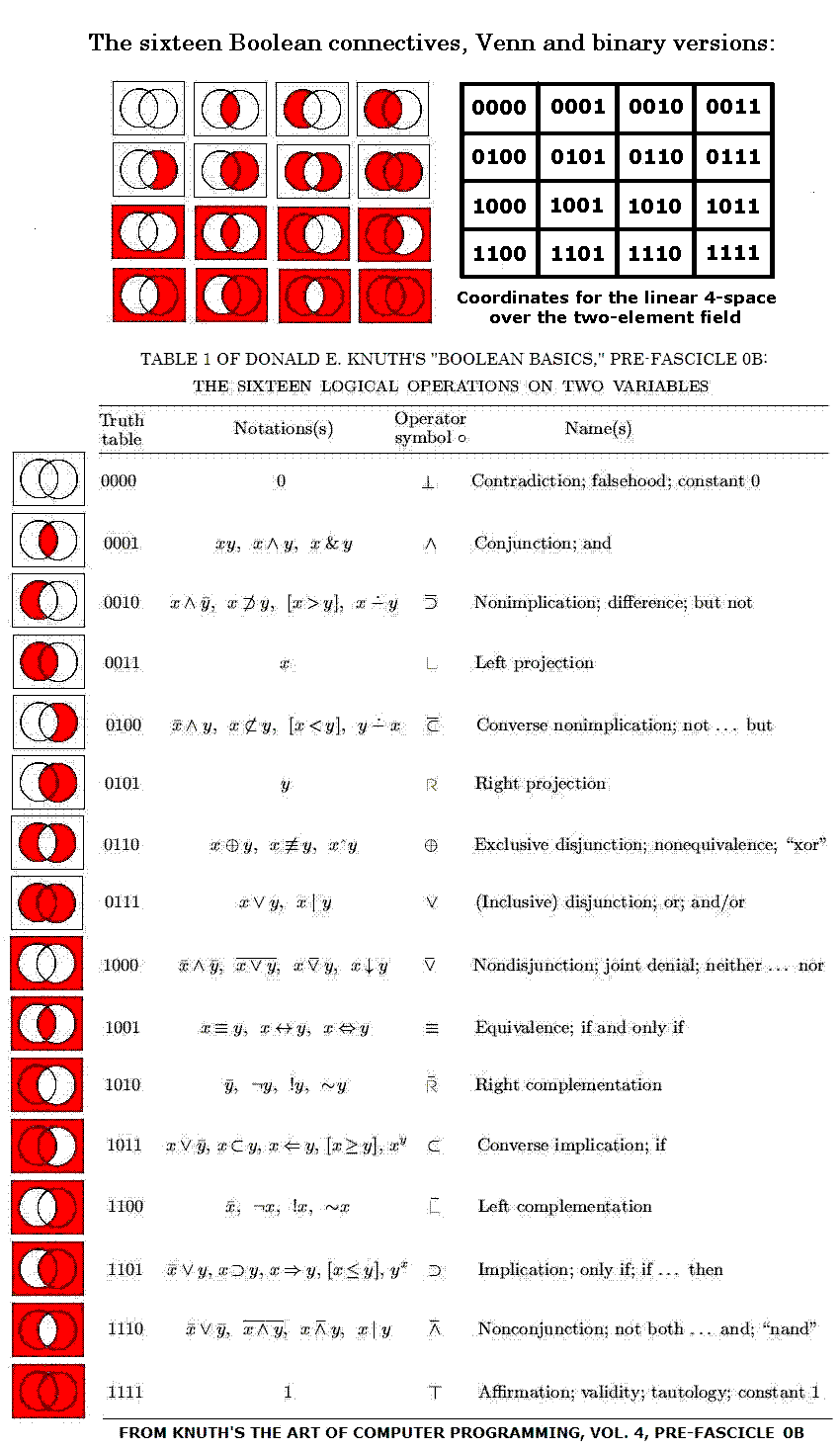
Figure 3
To recapitulate-- as noted previously, in Figure 2 viewed as a lattice-diagram the 16 digital labels 0000, 0001, etc., may be interpreted as naming the 16 subsets of a 4-set; in this case the partial ordering in the lattice is the structure preserved by the lattice's group of 24 automorphisms-- the same automorphism group as that of the 16 Boolean connectives.
If, however, the 16 digital labels are interpreted as naming the 16 functions from a 4-set to a 2-set (of two truth values, of two colors, of two finite-field elements, and so forth), it is not obvious that the notion of partial order is relevant. For such a set of 16 functions, the relevant group of automorphisms may be the affine group of A mentioned above. One might argue that each Venn diagram in Figure 3 constitutes such a function-- specifically, a mapping of four nonoverlapping regions within a rectangle to a set of two colors-- and that the diagrams, considered simply as a set of two-color mappings, have an automorphism group of order larger than 24... in fact, of order 322,560. Whether such a group can be regarded as forming part of a "geometry of logic" is open to debate.
Miller's talk refers to his earlier construction of a geometric space whose points are the propositions of a theory:
In ‘A Geometry of Logic’ (1984)...
I set out to be utterly literal, and to show how
single propositions (but not theories) may be
regarded as points in a metric or pseudometric
space. I presented three rather dissimilar
axiomatizations (one new, two well known) of
a pseudometrical theory of distance in Boolean
algebra, which is the canonical algebraic
representation of classical propositional logic.
As the above figures suggest, a rather different "utterly literal"
approach might involve, not a metric or pseudometric space, but instead
the finite geometry A.
In summary, geometrically-defined permutations acting on the 16 Boolean connectives have seemed, to some,* a nontrivial topic for study. The 4x4 space A provides a new** setting for such investigations, a setting that accommodates many more automorphisms than have previously been considered in what has been called "the geometry of logic."
* That mathematically unlearned authors such as Jean Piaget (see Jean-Blaise Grize's discussion of Piaget, "Operatory Logic," pp. 77-86 in Inhelder, De Caprona, and Cornu-Wells (eds.), Piaget Today, Psychology Press (UK), 1987) and Shea Zellweger (see his "Untapped Potential in Peirce's Iconic Notation for the Sixteen Binary Connectives", pp. 334–386 in Houser, Roberts, Van Evra (eds.), Studies in the Logic of Charles Sanders Peirce, Indiana University Press, Bloomington, IN, 1997) have discussed variants of the geometric-figure approach to Boolean automorphisms does not necessarily mean that it is unworthy of attention. For an approach more sophisticated than those of Piaget and Zellweger, see, for instance, Achille C. Varzi's "The Geometry of Negation" (with Massimo Warglien), Journal of Applied Non-Classical Logics, 13 (2003), 9-19. (Thanks to an anonymous Usenet author for this reference.)
|
Further details: A search for references to Zellweger leads to a detailed
description of a group of 16 "logical automorphisms" of the
16 binary connectives in the paper
"Simetria y Logica: La notacion de Peirce para los 16 conectivos
binarios," by Mireya
Garcia, Jhon Fredy Gomez, and Arnold Oostra. (Published in the Memorias
del XII Encuentro de Geometria y sus Aplicaciones,
Universidad Pedagogica Nacional, Bogota, June 2001; on the Web at http://www.unav.es/gep/Articulos/SimetriaYLogica.pdf.)
The authors do not identify this group as isomorphic to a subgroup of
the affine group of A;
this can serve as an exercise. The Oostra paper also suggests
an
introductory exercise for those unfamiliar with Boolean lattices:
determine whether the
authors' order-16 group includes all
transformations that might
reasonably
be called "logical automorphisms" of the 16 binary connectives. |
** Update of Sept. 12, 2007: There may be some question about the word "new" here. See, for instance, "Logic as a Vector System," by Jonathan Westphal and Jim Hardy, Journal of Logic and Computation 2005 15(5): 751-765. Westphal and Hardy said that "no one has, so far as we know, proposed modelling propositions as vectors while retaining classical logic." They discussed a system of arrow diagrams, superficially resembling vectors in a Euclidean space, that can be used to illustrate propositional logic. In contrast, the above affine space A over GF(2) is naturally associated (like any affine space) with a true vector space-- namely, the space of its translations. The 16 points of A may be regarded as elements of either the affine space or the vector space, depending on what sort of transformations they are to undergo.
Update of Sept. 27, 2007: The above association of the affine
4-space A with the 16 Boolean connectives is not
new. See, for
instance, Carol
von der Lin on Projective
Structures (unsigned, undated, web page, parts of which are from
Nov. 2003 or before). The resulting association of
the
Boolean connectives with group actions on the 4x4 square may, however,
be new.
For a much more sophisticated approach to geometry and logic,
see Steven
Vickers on geometric
logic.
Author: Steven H. Cullinane
Page created March 10, 2007. Last modified September 27, 2007.