"A guiding principle in modern mathematics is this lesson: Whenever you have to do with a structure-endowed entity S, try to determine its group of automorphisms, the group of those element-wise transformations which leave all structural relations undisturbed.  You can expect to gain a deep insight into the constitution of S in this way."

-- Hermann Weyl in Symmetry

Let us apply Weyl's lesson to the following "structure-endowed entity."

What is the order of the resulting group of automorphisms?

First, of course, we must determine exactly what "structural relations" we wish to leave undisturbed.

Trivially, the overall 4x4 structure is left undistubed by any permutation of the sixteen dots.  But not all substructures are left undistubed by an arbitrary permutation.  For example, the set of four rows and the set of four columns are left undisturbed by permutations of rows and/or columns, but not by permutations of the four 2x2 quadrants.

We may be interested in permutations that preserve the structural relation of adjacency.  In this case, it turns out that the group of symmetries of the four-dimensional hypercube, or tesseract,

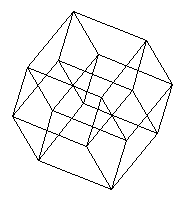
is what we are looking for, since it is well-known that adjacency in the hypercube is equivalent to adjacency in a 4x4 array-- provided we regard the array as drawn on a torus, so that each element of the array is adjacent to four other elements.  The hypercube's symmetry group is of order 384.

We may, however, be interested in structural relations other than adjacency.  For instance, we may be interested in families of subsets of the sixteen dots.

One such family, the 6-sets of the (16₆, 16₆) Kummer configuration, was discussed (without naming it as such) by R.D. Carmichael in 1937. For that configuration, see this website's note on Configurations and Squares.  Carmichael's 1937 classic, Introduction to the Theory of Groups of Finite Order, seems, however, to have overlooked an even more interesting family of subsets.

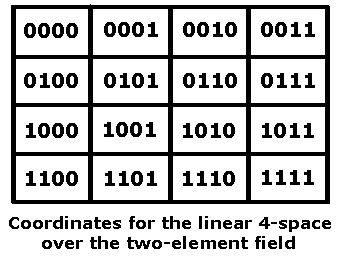
It turns out that if we regard the 4x4 array as a picture of the affine space of four dimensions over the two-element field, a very natural family of subsets is provided by the 35 partitions of the space into four parallel affine planes -- that is to say, into the 35 two-dimensional linear subspaces of a corresponding vector space and their cosets under translations. The illustration below shows these 35 structures.

Aficionados of T. S. Eliot may, if they like,
call the four-element planes or cosets "quartets."

For a description of how the 4x4 array can be coordinatized to yield this family of partitions and also a group of 322,560 permutations (rather than the measly 384 of the hypercube) that leave affine "structural relations" undisturbed, see Finite Relativity.

Strangely enough, this rather obvious geometric picture -- that of the linear four-space over the two-element field as a 4x4 array -- seems to have been completely overlooked in the refereed literature, except for its occurrence in the "miracle octad generator" (MOG) devised by R. T. Curtis* in his study of the Mathieu group M₂₄.  Even in that occurrence, the 4x4 parts of Curtis's 4x6 MOG arrays were neither supplied with coordinates nor, indeed, explicitly identified as possessing the structure of a finite geometry (although the appropriate group -- which provides a nice solution to Weyl's problem above -- was described, albeit in a non-geometric manner).

The Curtis MOG is a pairing of 35 partitions of a 4x4 array into four-sets (which turn out, once the array has been suitably coordinatized as a linear space, to be the cosets, under translation, of the 35 two-dimensional linear subspaces) with the 35 partitions of an eight-set (shown as an array of four rows and two columns) into two four-sets.  This pairing is not arbitrary; it is preserved under the action of the 244,823,040 permutations of the large Mathieu group M₂₄ acting on an array of four rows and six columns.  See published descriptions* of the MOG for details.

Within one of the maximal subgroups (a "brick stabilizer") of M₂₄, each of the 322,560 affine transformations of the 4x4 array is accompanied by a related M₂₄ action (the identity, if the affine transformation is a translation) on an associated 4x2 array, or "brick," of the MOG.  These group actions illustrate the well-known isomorphism (pdf) of the alternating group on eight elements, A₈, with the general linear group, GL(4,2), on the four-space over the two-element field.

One of the 35 pairs in the Curtis MOG

For a description of one way to construct the MOG,
see Generating the Octad Generator, from which
the following illustration is drawn.

How the MOG Works The quintuply transitive Mathieu group M24 is the automorphism group of the set of octads, or 8-sets, generated by the Curtis Miracle Octad Generator (MOG).  (See Peter J. Cameron's Geometry of the Mathieu Groups (pdf).) There are 759 such octads: (7 * 2 * 2 * 3) + (28 * 2 * 4 * 3) + 3 = 759, or, in symbols, (A * B * C * D) + ( E * F * G * H) + I = 759. Where the above numbers come from: Each octad occurs within a 24-set: an array of 4 rows and 6 columns.  This 4x6 array is made up of three 4x2 completely  interchangeable "bricks." Each brick, considered by itself, is an octad.  Hence the "I" value of 3, for the 3 individual bricks. A non-brick octad is formed by selecting 4 similarly marked locations (all black or all white) within one of the 35 4x2 MOG pictures, and 4 similarly marked locations (all black, all white, all circles, or all dots) in the corresponding 4x4 MOG picture, then applying a permutation (possibly the identity) of the three bricks of the resulting 4x6 array. Apart from the octads that are themselves bricks, the 8 cells that define an octad may occur in a 4 + 4 + 0 (or 4 + 0 + 4 or 0 + 4 + 4) pattern within the three bricks. or they may occur in a 4 + 2 + 2 (or 2 + 4 + 2 or 2 + 2 + 4) pattern within the three bricks. In the 4 + 4 + 0, etc., case, one of the two nonempty bricks in a 4x6 array contains 4 cells (either the four white or the four black cells) from one of the 7 bricks pictured in the leftmost column of the MOG picture, which can be chosen in 2 ways (hence "A" and "B"), and the other nonempty brick contains 4 cells (any 4 cells marked alike) from the corresponding picture in column 6 of the MOG; these 4 cells can fall within this nonempty brick in exactly 2 ways (hence "C").  Switching the two nonempty bricks adds no new octads.  The third, empty, brick can fall in any of the three brick positions (hence "D"). In the 4 + 2 + 2, etc., case, one of the 3 bricks, the "heavy" brick, contains 4 elements of the octad.  This can fall within any of the three brick positions (hence "H").  There are clearly 28 * 2 choices (from the MOG pictures in columns 2 through 5) for the 4 elements of the heavy brick (hence "E" and "F").  Paired with each of these choices are 4 ways of selecting the "2 + 2" elements in the other two bricks, based on the sets of 4 like elements in each of the MOG pictures in columns 7 through 10 (hence "G").  Switching the two "2 + 2" bricks adds no new octads.

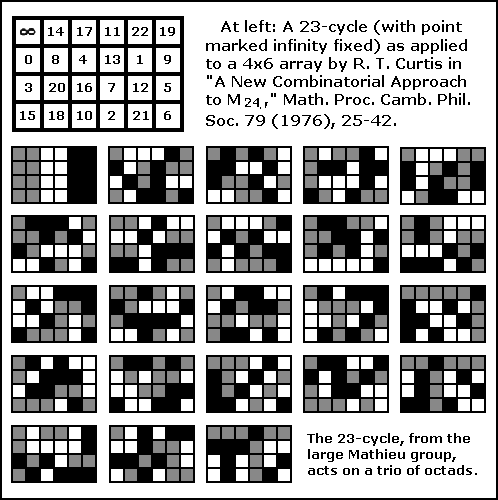
The illustration below shows the action
of a 23-cycle from M₂₄ on a "trio" of octads.

The Curtis MOG plays a prominent role in the book Twelve Sporadic Groups, by Robert L. Griess, which discusses some of the groups involved in Griess's Monster.**  A picture of a MOG action appears on the book's cover.  For some other connections between the MOG and the Monster, see the October 2004 paper Cross Orbits (pdf), by Peter Rowley.

For a description of how the 4x4 array also provides a nice picture of the 35 lines in the finite projective space PG(3,2) (as well as the 35 planes through a point in the finite affine space AG(4,2)), see Orthogonal Latin Squares as Skew Lines.

In fact, the MOG has an ancestor in the literature of finite projective geometry. A pairing equivalent to that in the MOG was described (though without the rectangular arrays devised by Curtis) in a paper on the projective space PG(3,2) published in 1910.  See page 72 of G. M. Conwell's "The 3-Space PG(3,2) and Its Group," Ann. of Math. 11 (1910), 60-76.

The relevant result is as follows:

"There exists a bijective correspondence between the 35 lines of PG(3,2) and the 35 unordered triples in a 7-set such that lines are concurrent if and only if the corresponding triples have exactly one element in common."

-- Elisabeth Kuijken, Thesis (ps), March 2003.

Kuijken cites Conwell as the source of this result. The result may be verified by examining the MOG illustration above in light of the note Orthogonal Latin Squares as Skew Lines.

For another approach to constructing the MOG that involves the symplectic generalized quadrangle known as W(2), see Picturing the Smallest Projective 3-space.

For a theorem illustrating a nice interplay between affine and projective substructures of the 4x4 array, see Map Systems.

It is conceivable that the decomposition strategy sketched in the "Map Systems" note might have some valuable generalizations.

The affine group in the 4x4 space can be generated by permuting rows, columns, and quadrants. For an illustration, see the Diamond 16 Puzzle.  For a proof, see Binary Coordinate Systems.  For some background, see Diamond Theory and Galois Geometry.

As noted above, the 4x4 square model
lets us visualize the projective space PG(3,2) as well as the affine space AG(4,2).  For tetrahedral and pentagonal (pdf) models of PG(3,2), see the work of Burkard Polster.  The following is from an advertisement of a talk by Polster on PG(3,2).

The Smallest Perfect Universe "After a short introduction to finite geometries, I'll take you on a... guided tour of the smallest perfect universe -- a complex universe of breathtaking abstract beauty, consisting of only 15 points, 35 lines and 15 planes -- a space whose overall design incorporates and improves many of the standard features of the three-dimensional Euclidean space we live in.... Among mathematicians our perfect universe is known as PG(3,2) -- the smallest three-dimensional projective space.  It plays an important role in many core mathematical disciplines such as combinatorics, group theory, and geometry." -- Burkard Polster, May 2001 See also my commentary on a paper by Polster.

Note on Required Background

"There is no royal road to geometry."
-- Saying attributed to Euclid

The reader is not expected to fully understand the above material unless he or she has had undergraduate instruction in linear algebra, abstract algebra, and modern geometry. The following references may, however, be helpful:

Books:

Contemporary Abstract Algebra, by Joseph A. Gallian

Geometry and Symmetry, by Paul B. Yale

Websites:

Groups and Symmetry, by Phill Schultz.
See especially Part 19, Linear Groups Over Other Fields.

As Schultz demonstrates, the order of the affine group in the four-dimensional space over the two-element field is

(2⁴)(2⁴ - 1)(2⁴ - 2¹)(2⁴ - 2²)(2⁴ - 2³) =
(16)(16 - 1)(16 - 2)(16 - 4)(16 - 8) =
(16)(15)(14)(12)(8) = 322,560.

Classical Groups, by Peter J. Cameron

Projective and Polar Spaces, by Peter J. Cameron

Finite Geometries (ps), by Juergen Bierbrauer

An Introduction to Finite Geometry (ps), by Simeon Ball

Finite Geometry (pdf), by Chris Godsil

Finite Geometry Web, resource listings by Alan Offer

Some Sporadic Geometries Related to PG(3,2) (jpg), by Arnold Neumaier

Sporadic Simple Groups (ps), by Simon Nickerson

* "A New Combinatorial Approach to M₂₄," by R. T. Curtis, Math. Proc. Camb. Phil. Soc. 79 (1976), pp. 25-42. For a more accessible discussion of the MOG, see Sphere Packings, Lattices, and Groups by Conway and Sloane.  For related material on octads, see the discussion of the (extended binary) Golay code in The Theory of Error-Correcting Codes by Sloane and MacWilliams.

** Properties of the 4x4 array can play at least a small introductory role in the amalgam, or Ivanov-Shpectorov (pdf), approach to some sporadic simple groups. See the following sequence of readings:

1. Inscapes, a 1982 note on picturing a symplectic polarity using 4x4 arrays, and a related 1986 note, Picturing the Smallest Projective 3-space.
2. The Sp(4,2) Generalized Quadrangle (html), by A. E. Brouwer.
3. Paper (pdf) by Burkard Polster containing a picture of the symplectic generalized quadrangle W(2) in pentagonal form, rather than the 4x4 form of (1) above.  See also my commentary on Polster's paper.
4. Some Constructions and Embeddings of the Tilde Geometry (pdf), by Antonio Pasini and Hendrick Van Maldeghem (a 2002 paper on "the flag transitive connected triple cover of the unique generalized quadrangle W(2) of order (2,2)").  Pasini and Van Maldeghem describe in detail how the tilde geometry is related to PG(3,2), AG(4,2), and the geometry of the Curtis MOG.
5. A 1994 AMS research announcement (pdf), by A. A. Ivanov and S. V. Shpectorov, on the role played by (generalized) tilde geometries in the study of various sporadic simple groups.

Page created March 18, 2004