"... die
Schönheit... [ist] die richtige Übereinstimmung der
Teile miteinander und mit dem Ganzen."
"Beauty is
the proper conformity of the parts to one another and to the whole."
-- Werner Heisenberg, "Die Bedeutung des Schönen in der
exakten Naturwissenschaft," address delivered to the Bavarian
Academy of Fine Arts, Munich, 9 Oct. 1970,
reprinted in Heisenberg's Across the Frontiers, translated by Peter
Heath, Harper & Row, 1974
"After the analysis which discovers the second quality
[symmetry,
following wholeness] the mind makes the only possible synthesis and
discovers the third quality [claritas or radiance]. This is the moment
which I call epiphany. First we recognise that the object is
one
integral thing, then we recognise that it is an organised composite
structure, a
thing
in fact: finally, when the relation of the parts is exquisite, when the
parts are adjusted to the special point, we recognise that it is
that
thing which it is. Its soul, its whatness, leaps to us from the
vestment of its appearance. The soul of the commonest object, the
structure of which is so adjusted, seems to us radiant. The object
achieves its epiphany."
-- James Joyce,
Stephen Hero, as quoted
by Jorn Barger
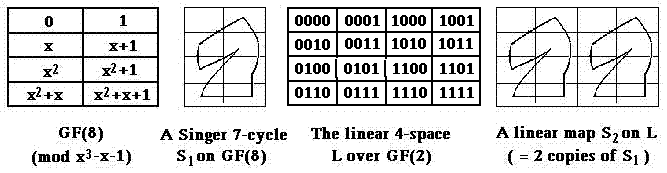
An important subset of the above
thirty-five 8-set partitions
may also be pictured
as follows:
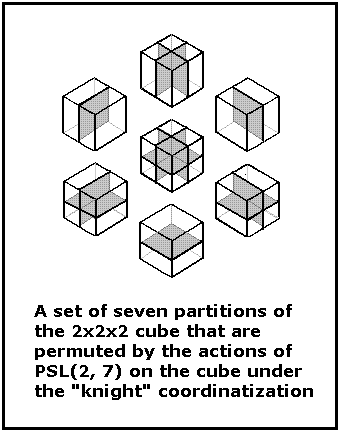
These seven partitions may also
be viewed as the seven points of
the finite projective plane
over the 2-element field.
See
The Eightfold Cube.
Joseph Payne, "Froebel and the Kindergarten
System of
Education" (lecture, Feb. 25, 1874) in Lectures on the Science and
Art of Education, with
Other
Lectures, New York and Chicago, E. L. Kellogg & Co., New
Edition, 1890, pp. 330-331--
"Then the examination of the cube,
especially its surfaces, edges, and angles, which any child can observe
for himself, suggest [sic] new sensations and their resulting
perceptions. At the same time, notions of space, time, form, motion,
relativity in general, take their place in the mind, as the unshaped
blocks which, when fitly compacted together, will lay the firm
foundation of the understanding. These elementary notions, as the very
groundwork of mathematics, will be seen to have their use as time goes
on.
The third Gift is a large cube, making a whole, which is
divisible into eight small ones. The form is recognized as that of the
cube before seen; the size is different. But the new experiences
consist in notions of relativity-- of the whole in its relation to the
parts, of the parts in their relation to the whole; and thus the child
acquires the notion and the names, and both in immediate connection
with the sensible objects, of halves, quarters, eighths, and of how
many of the small divisions make one of the larger. But in
connection with the third Gift a new faculty is called forth--
Imagination-- and with it the instinct of construction is awakened."
Part III:
A somewhat different use
of the term "relativity"--
The Relativity Problem
"This is the relativity problem: to fix objectively a
class of equivalent coordinatizations and to ascertain the group of
transformations S mediating between them."
-- Hermann Weyl,
The Classical Groups, Princeton University
Press, 1946, p. 16
For some related remarks on coordinatizations that
apply to the eightfold cube as well as to larger structures, see
Finite
Relativity.
From some 1949 remarks of Weyl:
"The
relativity problem is one of central significance throughout geometry
and algebra and has
been recognized as such by the mathematicians at an early time."
-- Hermann Weyl, "Relativity Theory as a Stimulus in Mathematical Research,"
Proceedings of the American Philosophical Society,
Vol. 93, No. 7, Theory of Relativity in Contemporary Science:
Papers
Read at the Celebration of the Seventieth Birthday of Professor Albert
Einstein in Princeton, March 19, 1949 (Dec. 30, 1949), pp. 535-541
Page created January 16, 2008.