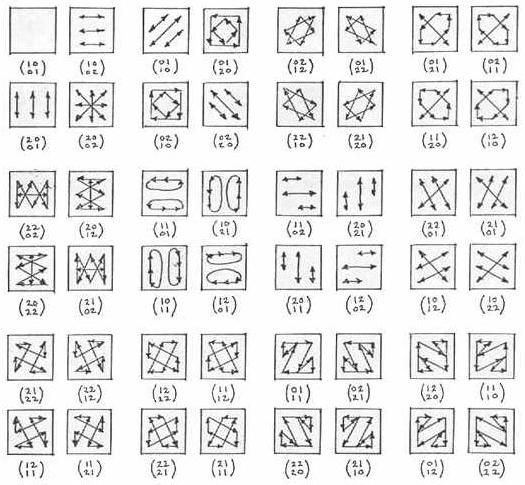
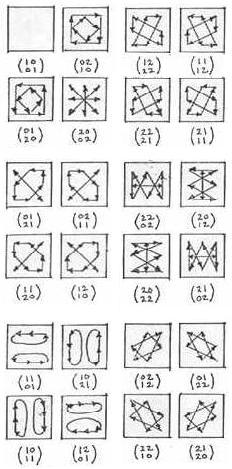
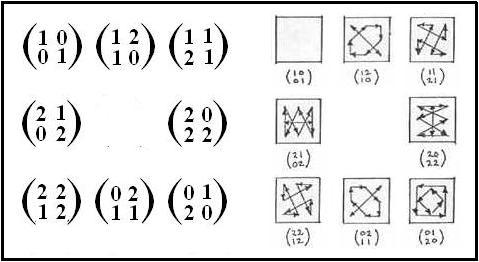
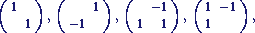This web page contains
a note from 1985 followed by
remarks on some of the groups, and a non-Desarguesian translation
plane, implicit in that note. --Steven H. Cullinane, August 28, 2005
Updates:
For a neater version of the pictures in the 1985
note, see
GL(2,3),
by Nick Wedd.
August 19, 2009--
For a program by Ed Pegg Jr. at Wolfram.com that extends the example
from 1985 shown below to many, many more group actions on small
coordinate arrays, see
Group Actions,
1984-2009.
August 19-20, 2009--
The above-mentioned group actions illustrated at Wolfram.com-- GL(2,p)
where p keeps increasing-- suggest a
natural
modification of the 1985 note "Visualizing GL(2,p)"-- Replace p by Z.
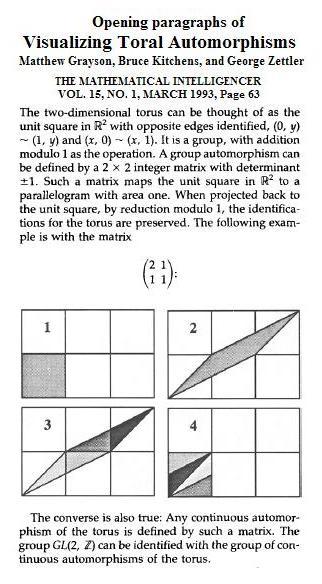
See "
Visualizing
Toral Automorphisms," by Matthew Grayson, Bruce Kitchens, and
George Zettler,
Mathematical Intelligencer, Volume 15, Number
1, March 1993 (illustrated below):
"The group GL(2,Z) can be identified with the group of
continuous automorphisms of the torus."
Historically, of course, visualization of GL(2,Z) preceded that of
GL(2,p). See, for instance, the Wikipedia article on
Arnold's Cat Map
and especially its illustration (
animated gif,
3.5 mb) of a discrete version of an iterated toral automorphism
applied to a picture of a
pepper.