Finite Geometry Notes   | Home | Site Map | Author |
 
Group Actions, 1984-2009
by Steven H. Cullinane on August 19, 2009

From a 1984 book review:

"After three decades of intensive research by hundreds of group theorists, the century old problem of the classification of the finite simple groups has been solved and the whole field has been drastically changed. A few years ago the one focus of attention was the program for the classification; now there are many active areas including the study of the connections between groups and geometries, sporadic groups and, especially, the representation theory. A spate of books on finite groups, of different breadths and on a variety of topics, has appeared, and it is a good time for this to happen. Moreover, the classification means that the view of the subject is quite different; even the most elementary treatment of groups should be modified, as we now know that all finite groups are made up of groups which, for the most part, are imitations of Lie groups using finite fields instead of the reals and complexes. The typical example of a finite group is GL(n, q), the general linear group of n dimensions over the field with q elements. The student who is introduced to the subject with other examples is being completely misled."

-- Jonathan L. Alperin,
   review of books on group theory,
   Bulletin (New Series) of the American
   Mathematical Society 10 (1984) 121, doi:
   10.1090/S0273-0979-1984-15210-8

A more specific example:
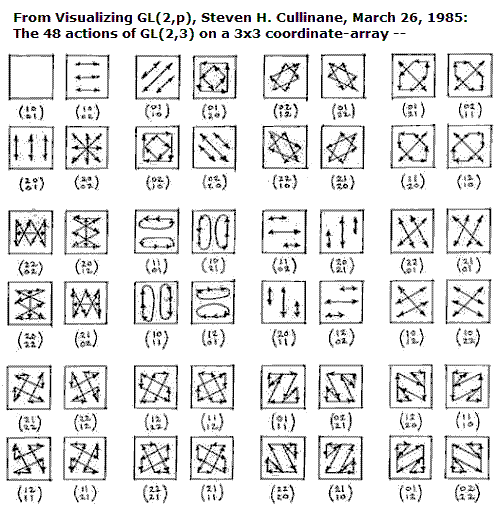
Actions of GL(2,3) on a 3x3 coordinate-array

The same example
at Wolfram.com:

Ed Pegg Jr.'s program at Wolfram.com to display a large number of actions of small linear groups over finite fields
Caption from Wolfram.com:

"The two-dimensional space Z3×Z3 contains nine points: (0,0), (0,1), (0,2), (1,0), (1,1), (1,2), (2,0), (2,1), and (2,2). The 48 invertible 2×2 matrices over Z3 form the general linear group known as GL(2, 3). They act on Z3×Z3 by matrix multiplication modulo 3, permuting the nine points. More generally, GL(n, p) is the set of invertible n×n matrices over the field Zp, where p is prime. With (0, 0) shifted to the center, the matrix actions on the nine points make symmetrical patterns."

Citation data from Wolfram.com:

"GL(2,p) and GL(3,3) Acting on Points"
 from The Wolfram Demonstrations Project,
 http://demonstrations.wolfram.com/GL2PAndGL33ActingOnPoints/,
 Contributed by: Ed Pegg Jr"

As well as displaying Cullinane's 48 pictures of group actions from 1985, the Pegg program displays many, many more actions of small finite general linear groups over finite fields. It illustrates Cullinane's 1985 statement:
"Actions of GL(2,p) on a p×p coordinate-array have the same sorts of symmetries, where p is any odd prime."
Pegg's program also illustrates actions on a cubical array-- a 3×3×3 array acted on by GL(3,3). For some other actions on cubical arrays, see Cullinane's Finite Geometry of the Square and Cube.