Finite Geometry Notes   | Home | Site Map | Author |

The Galois Tesseract

by Steven H. Cullinane on Sept. 3, 2011*
It is well-known** that the 16 elements of  a 4x4 array
may, when opposite edges of the array are identified,
be regarded as the 16 vertices of a tesseract.

Square array and tesseract. Array's 16 cells and tesseract's 16 vertices have corresponding adjacencies.

The interplay of algebraic and geometric properties within the 4x4 array that
forms two-thirds of the Curtis Miracle Octad Generator (MOG) may first have
been described by Cullinane (AMS abstract 79T-A37, Notices , Feb. 1979).

The following image gives some further details.
IMAGE- The Galois Tesseract in SPLAG

Here is some supporting material—

IMAGE- Carmichael, Conway, and Curtis on the Galois Tesseract

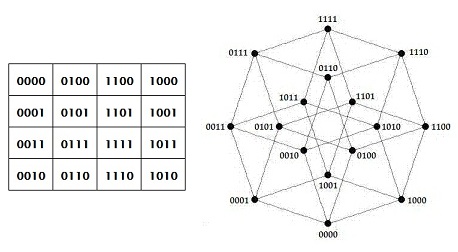
The passage from Carmichael above emphasizes the importance of
the 4x4 square within the MOG.

The passage from Conway and Sloane, in a book whose first edition
was published in 1988, makes explicit the structure of the MOG's
4x4 square as the affine 4-space over the 2-element Galois field.

The passage from Curtis (1974, published in 1976) describes 35 sets
of four "special tetrads" within the 4x4 square of the MOG. These
correspond to the 35 sets of four parallel 4-point affine planes within
the square. Curtis, however, in 1976 makes no mention of the affine
structure, characterizing his 140 "special tetrads" rather by the parity
of their intersections with the square's rows and columns.

The affine structure appears in the 1979 abstract mentioned above—

IMAGE- An AMS abstract from 1979 showing how the affine group AGL(4,2) of 322,560 transformations acts on a 4x4 square

The "35 structures" of the abstract were listed, with an application to
Latin-square orthogonality, in a note from December 1978—

IMAGE- Projective-space structure and Latin-square orthogonality in a set of 35 square arrays

(These 35 structures comprise, it turns out, the Rosenhain and Göpel tetrads
described by R. W. H. T. Hudson in his 1905 classic Kummer's Quartic Surface.
See Rosenhain and Göpel tetrads in PG(3,2).)

See also a 1987 article by R. T. Curtis—

Further elementary techniques using the miracle octad generator, by R. T. Curtis.

Abstract:

“In this paper we describe various techniques, some of which are already used by devotees of the art, which relate certain maximal subgroups of the Mathieu group M24, as seen in the MOG, to matrix groups over finite fields. We hope to bring out the wealth of algebraic structure* underlying the device and to enable the reader to move freely between these matrices and permutations. Perhaps the MOG was mis-named as simply an ‘octad generator’; in this paper we intend to show that it is in reality a natural diagram of the binary Golay code.”

(Received July 20 1987)

– Proceedings of the Edinburgh Mathematical Society (Series 2) (1989), 32: 345-353

* For instance:

Algebraic structure in the 4x4 square, by Cullinane (1985) and Curtis (1987)

The following 1955 review of  a 1954 paper by W. L. Edge,  "The Geometry of the Linear Fractional Group LF(4,2)," brings out the wealth of geometric structure underlying the Curtis device. The 35 line-diagram structures pictured above provide another approach to this geometric structure and to the algebraic (diamond ring) structure of the Galois tesseract. 

W. L. Edge on the geometry of the projective 3-space over GF(2)

 * Last modified on March 24, 2013.

 ** See, for instance, Coxeter's 1950 "Self-Dual Configurations and Regular Graphs," 
      Bull. Amer. Math. Soc. vol. 56, pp. 413-455, figures 5 and 6 on p. 415.