Theme and Variations
"...the source of all great mathematics is the special case, the concrete example. It is frequent in mathematics that every instance of a concept of seemingly great generality is in essence the same as a small and concrete special case."
-- Paul Halmos in
I Want To Be a Mathematician
The great mathematician Hermann Weyl wrote a book, Symmetry, to make the point that visual symmetry is a special case of the concept known as invariance.
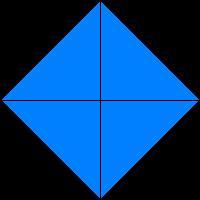
(An invariant is something that does not change under a set of transformations. Invariance is the property of being an invariant. Some felt that Einstein's relativity theory should be called Invariantentheorie, "theory of invariants.")However you rearrange the quadrants of the diamond figure, the result has some ordinary or color-interchange symmetry:
So the diamond figure illustrates how symmetry itself can be invariant under a set of tranformations.
This would be of little interest unless this invariance of symmetry can be generalized. Fortunately, it can.-- Steven H. Cullinane
Related Material
|
|
From Diamond Theory, 1976 -- Variations  on the diamond theme: Quartets
"The more familiar we become with Four Quartets... the more we realize that the analogy with music goes much deeper than a comparison of the sections with the movements of a quartet, or than an identification of the four elements as 'thematic material.' One is constantly reminded of music by the treatment of images...." |
Page created April 28, 2004
For a large downloadable folder
containing this and many related web pages,
see Notes on Finite Geometry.