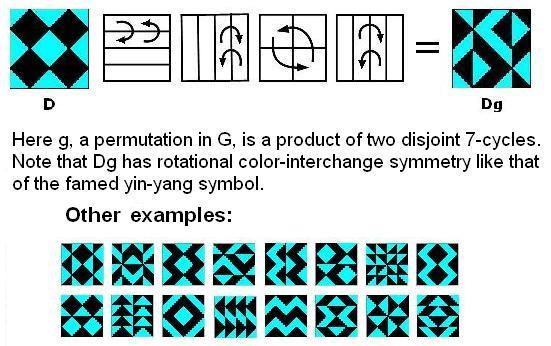
Towards a Philosophy of Real Mathematics, by David Corfield, Cambridge U. Press, 2003, p. 206:
“Now, it is no easy business defining what one means by the term conceptual…. I think we can say that the conceptual is usually expressible in terms of broad principles. A nice example of this comes in the form of harmonic analysis, which is based on the idea, whose scope has been shown by George Mackey (1992) to be immense, that many kinds of entity become easier to handle by decomposing them into components belonging to spaces invariant under specified symmetries.”
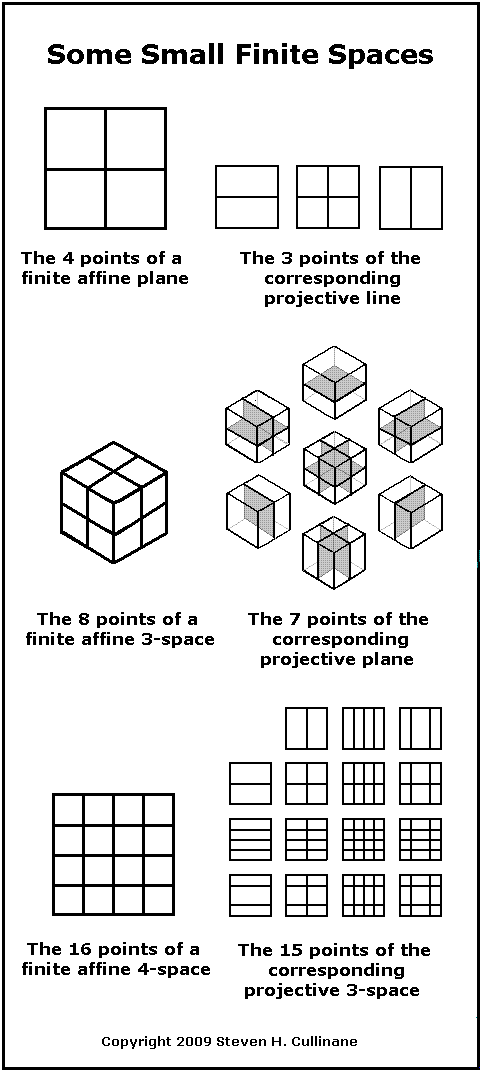
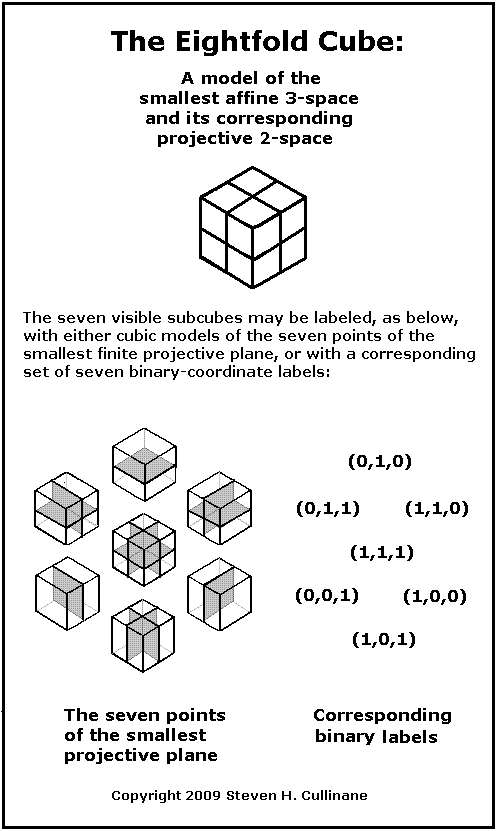
For a simpler example of this idea, see the entities in The Diamond Theorem, the decomposition in A Four-Color Theorem, and the space in Geometry of the 4×4 Square. The decomposition differs from that of harmonic analysis, although the subspaces involved in the diamond theorem are isomorphic to Walsh functions– well-known as discrete analogues of the trigonometric functions of traditional harmonic analysis.