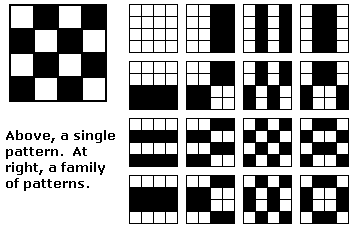
Finite Geometry Notes   | Home | Site Map | Author |

Pattern Groups:
Notes Toward a Definition

by Steven H. Cullinane

(Page created Oct. 2, 2005; last modified March 5, 2009.)

Some groups of transformations of square and rectangular arrays preserve interesting families of subsets of the arrays.  Subsets in the preserved families may, for instance, be symmetric, even though the transformations are themselves asymmetric and discontinuous.  Similarly for cubical arrays.

The relevant links:

Geometry of the 4x4 Square   The Diamond 16 Puzzle
The Eightfold Cube The Diamond Theorem
Diamond Theory Notes on Finite Geometry

In the 1970's, R. T. Curtis discovered that the large Mathieu group may be represented as a group of discontinuous transformations acting on a rectangular 4x6 array of square cells, or tiles, in such a way that the Carmichael-Witt family of 759 "octads" forming a Steiner system S(5,8,24), previously known to be preserved by the large Mathieu group, appears as a family of geometrically natural subsets of the rectangular array.  The relevant paper:
Curtis, R. T., A new combinatorial approach to M24, Math. Proc. Camb. Phil. Soc. 79 (1976), pp. 25-42
For details of how the Curtis model of the 759 octads is related to a group of 322,560 symmetry-preserving discontinuous transformations of a 4x4 array of square tiles, see Geometry of the 4x4 Square.

These groups act on square cells, or tiles, but discontinuous transformations may also act on, say, plane 2-colored tilings by equilateral triangles, with each triangle all black or all white; permutations of the triangles are induced by permutations of the triangles' centers.  Groups of such discontinuous transformations may preserve families of two-colored infinite plane patterns, each of which has some symmetry. Groups of discontinuous transformations may, of course, also act on tilings of non-Euclidean surfaces such as the hyperbolic plane.

There is as yet no general theory of families of patterns (i.e., of families of subsets) invariant under discontinuous transformations acting on plane or 3-space tilings.

An elementary example:

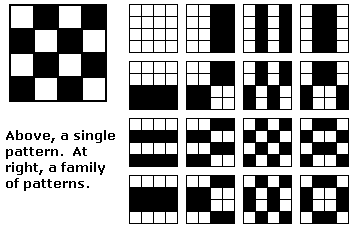
Pattern and family of patterns

The above observations may contribute to the beginnings of such a theory. Clearly, letting a family of patterns generate a vector space under binary addition (i.e., symmetric difference of subsets) is a central strategy. What geometric properties of such vector spaces we may expect to emerge under group actions is, as the work of Curtis shows, not so clear. It seems that such a general theory of pattern-invariance might throw some additional light on such phenomena as the connection of the affine hyperplanes that underlie the diamond theorem with the Curtis model of the 759 octads (which includes versions of those affine hyperplanes).

Since n×n square patterns of black and white cells-- i.e., (0,1)-matrices-- are, essentially, binary relations on a finite set, such a theory would be rather closely related to the 1938 work of Marc Krasner on certain Galois connections:

From Ferdinand Börner, Martin Goldstern, and Saharon Shelah,
Automorphisms and strongly invariant relations (pdf),
a preprint dated Sept. 9, 2003

The image “Krasner.jpg” cannot be displayed, because it contains errors.

(Related material: A. Schleiermacher,
"Über einen Satz von Krasner,"
1. Teil (pdf) and 2. Teil (pdf))

See also Roger Duncan Maddux, Relation Algebras (Elsevier, 2006).

Related material may be found by a Google search on, say, "Galois connection" + "permutation group" + "relation."

What might be a suitable name for such a theory of patterns?  "Discontinuous transformations" seems both too general and too close to the name of another theory, that of "discontinuous (i.e., discrete) groups."  "Tiling groups" is already taken.  The name "pattern groups" seems brief, descriptive, and reasonably new.

Note that the above-mentioned work of R. T. Curtis shows that under a suitably inclusive definition of pattern, the large Mathieu group is a "pattern group"-- i.e., a group of automorphisms of a pattern (that is, a subset), or a family of patterns, or a family of families* of patterns, etc.

(Some restriction in the definition is needed to prevent every finite group being called a "pattern group," since every finite group may be represented as a group of discontinuous transformations acting on square (0,1)-matrices, i.e., on permutation matrices-- "patterns" of a sort.  It is not, however, clear what this restriction should be.)

The name "pattern groups" also serves to correct a serious error at the heart of what at first glance appears to be a closely related treatise:
Branko Grunbaum and G. C. Shephard,
Tilings and Patterns, W. H. Freeman and Co.,
New York 1987
Grunbaum and Shephard say that

"In every civilization and culture, colored tilings and patterns appear among the earliest decorations.... An early paper with remarkable counterchange designs formed by diagonally divided squares -- one-half black, one-half white -- was published by Truchet [1704]. For a more recent treatment, with many illustrations, see Cullinane [1976]. However, all these were more or less 'accidental' occurrences, independently reinvented many times.... The only artist who deliberately and consistently tried to investigate colored patterns (more specifically, colored tilings) was M. C. Escher...."

-- Pages 463 and 464; the "Cullinane [1976]" reference is to a preprint, "Diamond Theory," named on page 661.

The statement that "Cullinane [1976]" was "accidental" and not "deliberate and consistent" is an error... An understandable error, since the mathematics in the 1976 preprint and a later 1979 abstract (see The Diamond Theorem) involves a level of sophistication (matrix algebra over Galois fields) that Grunbaum and Shephard clearly lack.

* On "families of families" of subsets

From: Robin Chapman 
Subject: Re: Automorphism group of S_n
Date: Sun, 11 Feb 2001 10:26:17 GMT
Newsgroups: sci.math

In article <20010210221446.08836.00000412@ng-co1.news.gateway.net>,
  jamesrheckman@gateway.netnospam (Jim Heckman) wrote:
>
> Yeah, I've seen that in a few places. Perhaps more to the OP's
> point is actually constructing Aut(S_6), which I've only seen done
> by laboriously exploring the detailed structure of S_6, or by
> making use of the (not obvious) isomorphism between A_6 and
> PSL(2,9) -- which requires knowing a lot about finite groups of
> Lie type. Is there a "simple" way to construct Aut(S_6), or at least
> to show that its order is 2*|S_6|?

The argument used to show that Aut(S_n) is usually S_n gives you that
Aut(S_6) has order |S_6| or 2|S_6|. So we have to find an automorphism
of S_6 not an inner automorphism. The classical approach is due to
Sylvester (or was it Cayley)?

S_6 acts on the numbers 1, 2, 3, 4, 5, 6. A duad is an unordered
pair of these numbers, eg 13 or 25. S_6 acts on these. A syntheme
is an unordered triple of disjoint duads e.g. 13/25/46. S_6 acts
on these too. A synthematic total is an unordered quintuple of
synthemes incorporating all 15 duads, e.g
13/25/46//14/26/35//12/34/56//15/24/36//16/23/45.
There are 15 duads, 15 synthemes and 6 synthematic totals.
Each permutation of S_6 gives rise to a permutation of the duads,
of the synthemes and of the synthematic totals. Labelling the
totals arbitrarily from 1 to 6 we see that each element of S_6 gives
rise to another via the permutation of the totals. Thus we get
a homomorphism from S_6 to S_6 which we see cannot be trivial.
But we can check
that a transposition (i j) permutes the totals without fixed points
so this automorphism is not linear.

The whole setup can be reversed. Each duad of totals corresponds to a
syntheme. Each syntheme of totals correponds to a duad and each
synthematic total of totals corresponds to a number. If we look at the
permutations of the set {numbers} u {totals} preverving the "structure"
we get a group of order 1440 having S_6 as a subgroup. This is
Aut(S_6).

-- Source:
http://www.math.niu.edu/~rusin/known-math/01_incoming/aut_S6

For related material, see "The alternating group of degree 6 in geometry of the Leech lattice and K3 Surfaces" (pdf) by Jonghae Keum, Keiji Oguiso, and De-Qi Zhang.

Update of March 5, 2009:

Since this page was created, others have used the phrase "pattern group" with a different meaning:

From "Supercharacter Formulas for Pattern Groups," by Persi Diaconis and Nathaniel Thiem, preprint of Oct. 4, 2006:

Let Un(Fq) be the group of uppertriangular n × n matrices with entries in the finite field Fq, and with ones on the diagonal....

The primary focus of this paper is on a large class of subgroups called pattern subgroups. Let J ⊆ {(i, j) | 1 ≤ i < j ≤ n} be a subset that is closed in the sense that (i, j), (j, k) ⊆ J implies (i, k) ⊆ J (i.e. J is a partial order on {1, 2, . . . , n}). The pattern group UJ is the subgroup of Un(Fq) consisting of matrices whose (i, j)th entry is permitted to be nonzero only if (i, j) ∈ J.

Page created October 2, 2005.