The Klein Correspondence,
Penrose Space-Time,
and a Finite Model
Notes by Steven H. Cullinane
May 28, 2007
Part I: A Model of Space-Time
The following paper includes a figure illustrating
Penrose's
model of "complexified, compactified Minkowski
space-time as the Klein quadric in complex projective 5-space."
For some background on the Klein quadric and space-time, see Roger
Penrose, "
On the Origins
of Twistor Theory," from
Gravitation and Geometry:
A
Volume in Honor of Ivor Robinson, Bibliopolis, 1987.
Part II: A Corresponding Finite Model
The Klein quadric also occurs in a finite
model of projective 5-space. See a 1910 paper:
G. M. Conwell, The
3-space PG(3,2) and its group, Ann. of Math. 11,
60-76.
Conwell discusses the quadric, and the related Klein correspondence,
in detail. This is noted in a more recent paper by Philippe Cara:
As Cara goes on to explain, the Klein correspondence underlies
Conwell's discussion of eight
heptads. These play an
important role in another correspondence, illustrated in the
Miracle Octad
Generator of R. T. Curtis, that may be used to picture actions
of the large Mathieu group M
24.
Some background on heptads:
Edge on Heptads
Part I: Dye on Edge
"Summary:
....we obtain various orbits of partitions of quadrics over GF(2a)
by their maximal totally singular subspaces; the corresponding
stabilizers in the relevant orthogonal groups are investigated. It is
explained how some of these partitions naturally generalize Conwell's
heptagons for the Klein quadric in PG(5,2)."
"Introduction:
In 1910 Conwell... produced his heptagons in PG(5,2) associated
with the Klein quadric K whose points represent the lines of PG(3,2)....
Edge... constructed the 8 heptads of complexes in PG(3,2) directly.
Both he and Conwell used their 8 objects to establish geometrically the
isomorphisms SL(4,2)=A8 and O6(2)=S8 where O6(2) is the group of K...."
-- "Partitions and Their Stabilizers for Line Complexes and
Quadrics," by R.H. Dye, Annali di Matematica Pura ed Applicata,
Volume 114, Number 1, December 1977, pp. 173-194
Part II: Edge on Heptads
"The Geometry of the Linear Fractional Group LF(4,2),"
by W.L. Edge, Proc. London Math Soc., Volume s3-4, No. 1, 1954,
pp. 317-342. See the historical remarks on the
first page.
Note added by Edge in proof:
"Since this paper was finished I have found one by G. M. Conwell: Annals
of Mathematics (2) 11 (1910), 60-76...." |
The projective space PG(5,2), home of
the Klein quadric in the finite model, may be viewed as the set of 64
points of the affine space AG(6,2), minus the origin.
The 64 points of this affine space may in turn be viewed as the 64
hexagrams of the Classic of Transformation, China's I Ching.
There is a natural correspondence between the 64 hexagrams and the 64
subcubes of a
4x4x4 cube. This correspondence leads to a natural way to
generate the affine group AGL(6,2). This may in turn
be viewed as a group of over a trillion natural
transformations of the 64 hexagrams.
Geometry of
the I Ching.
"Once Knecht confessed to his teacher that he wished
to learn enough to be able to incorporate the system of the
I Ching
into the Glass Bead Game. Elder Brother laughed. 'Go ahead
and try,' he exclaimed. 'You'll see how it turns out.
Anyone can create a pretty little bamboo garden in the world. But
I doubt that the gardener would succeed in incorporating the world in
his bamboo grove.'"
Transcript of relevant text for search
engines:
Part I--
From "Twistor cosmology and quantum space-time," by Dorje
C. Brody
(Imperial College, London) and Lane P. Hughston (King's College London):
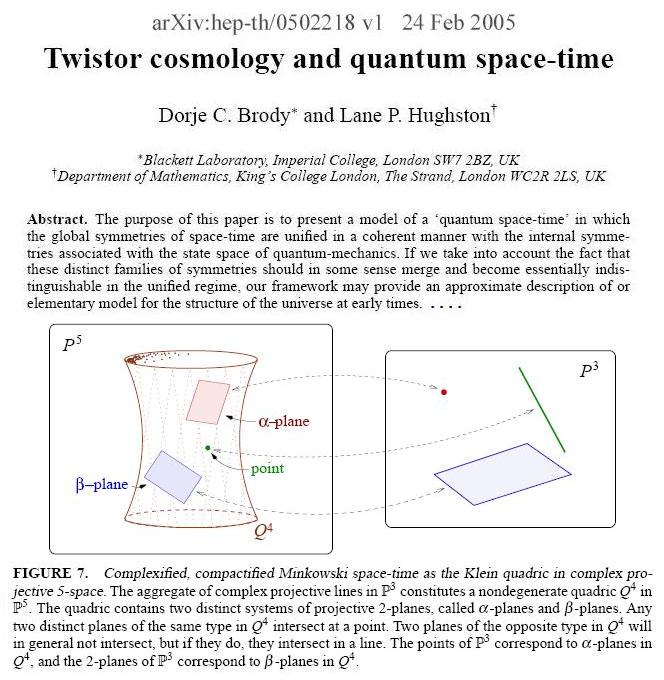
FIGURE 7. Complexified, compactified Minkowski space-time as the
Klein quadric in complex projective 5-space. The aggregate of
complex projective lines in P3 constitutes a nondegenerate
quadric Q4 in P5.
The quadric contains two distinct systems of projective 2-planes,
called alpha-planes and beta-planes. Any two distinct planes of the
same type in Q4 intersect at a point. Two planes of
the opposite type in Q4 will in general not
intersect, but if they do, they intersect in a line. The points of P3
correspond to alpha-planes in Q4, and the 2-planes
of P3 correspond to beta-planes in Q4.
Published in XIX Max Born Symposium, Wroclaw
(Poland), 28 September - 1 October
2004, Springer, 2004, pp. 57-95
Part II--
From "RWPRI Geometries for the alternating group A8,"
by Philippe Cara, Department of Mathematics, Vrije Universiteit Brussel
8.2. The Klein quadric
It is well known that the lines of PG(3,2) correspond
to the 35 points of a hyperbolic quadric Q+(5,2)
with equation
X0 X1 + X2 X3
+ X4 X5 = 0
in the five-dimensional projective space PG(5,2). This
correspondence is known as the Klein correspondence and the
hyperbolic quadric is then called the Klein quadric. In what
follows, the Klein quadric will be denoted by Q. On Q
there are two families of 15 planes each, which correspond to the 15
points and the 15 planes of PG(3,2) respectively. Two different
planes of the same family have one point in common and two planes of
different families are either disjoint or share one line. A
{point, plane}-flag p*P of PG(3,2) appears on Q
as two planes from different families which intersect in a line,
representing the three lines in PG(3,2) which are included in P
and contain the point p. The Klein correspondence for PG(3,2)
is described in detail in [14].
[14] G. M. Conwell, The 3-space PG(3,2) and its
group, Ann. of Math. 11 (1910), pp. 60-76
Published in Finite
Geometries: Proceedings of the Fourth Isle of Thorns Conference
(July 2000), Springer, 2001, ed. Aart
Blokhuis, James W. P. Hirschfeld, Dieter Jungnickel, and Joseph A.
Thas, pp. 61-97