Finite Geometry Notes   | Home | Site Map | Author |

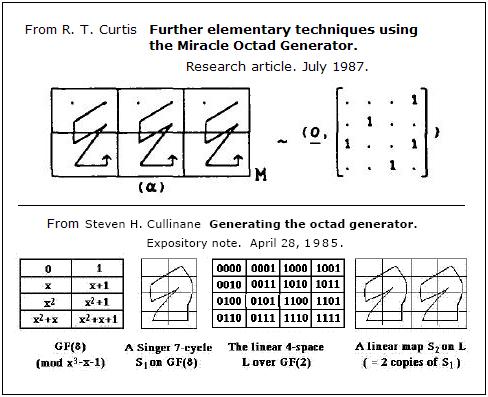
The Miracle Octad Generator
(MOG) of R T. Curtis

"By far the most important structure in design theory is the Steiner system S(5, 8, 24)."

-- "Block Designs," by Andries E. Brouwer (Ch. 14 (pp. 693-746) of Handbook of Combinatorics, Vol. I, MIT Press, 1995, edited by Ronald L. Graham, Martin Grötschel, and László Lovász, Section 16 (p. 716))

The image “MOGCurtisPlain.gif” cannot be displayed, because it contains errors.

Shown above is a rearranged version of the
Miracle Octad Generator (MOG) of R. T. Curtis
("A new combinatorial approach to M24,"
Math. Proc. Camb. Phil. Soc., 79 (1976), 25-42.)

The MOG is a pairing of the 35 partitions of an 8-set into two 4-sets with the 35 partitions of AG(4,2) (the affine 4-space over GF(2)) into 4 affine planes.  The pairing preserves certain incidence properties.  It is used in studying the Steiner system S(5, 8, 24), the large Mathieu group, the extended binary Golay code, the Leech lattice, and subgroups of the Monster.

History:

This pairing, without illustrations, was apparently first described in 1910 by G. M. Conwell in "The 3-space PG(3,2) and its group," Ann. of Math. 11 (1910) 60-76.

The 35 square structures above apparently first appeared, without any reference to their role in finite geometry, in the 1976 Curtis paper mentioned above.

The 35 square structures above were discovered independently in 1976 by Steven H. Cullinane.  The role they play in finite geometry was apparently first described by Cullinane in an AMS abstract in 1979 that was received for publication on Oct. 31, 1978. The connection between finite geometry and the square structures illustrated above was also pointed out by Cullinane in a note, "Orthogonal Latin Squares as Skew Lines," of December 1978.  (For related material, see Latin-Square Geometry.)  The existence of the 35 combinatorially defined square structures of Curtis was pointed out by Curtis to Cullinane in a personal communication of March 1979.  The connection between the finite-geometry research of Conwell and the combinatorial research of Curtis was apparently first pointed out in "Generating the Octad Generator," a note by Cullinane of April 28, 1985.

Curtis uses the MOG to construct the Steiner system S(5, 8, 24), a structure that goes back at least to Witt in 1938 and possibly (Rotman, An Introduction to the Theory of Groups) to Carmichael in 1931.  Uenal Mutlu cites specific papers that seem to be relevant:  R. D. Carmichael, "Tactical configurations of rank two," Amer. J. Math. 53 (1931) 217-240, and E. Witt, "Ueber Steinersche Systeme," Abh. Math. Sem. Hansischen Univ. 12 (1938) 265-275.

From Vol. II of Projective Geometry, a 1918 classic by Oswald Veblen, a line of thought that may help to understand the construction of the MOG:
Excerpt from Chapter III, "The Affine Group in the Plane"--

"The system of definitions and theorems which expose properties invariant under a given group of transformations may be called, in agreement with the point of view expounded in Klein's Erlangen Programm,* a geometry.  Obviously, all the theorems of the geometry corresponding to a given group continue to be theorems in the geometry corresponding to any subgroup of the given group; and the more restricted the group, the more figures will be distinct relatively to it, and the more theorems will appear in the geometry.  The extreme case is the group corresponding to the identity, the geometry of which is too large to be of consequence.

For our purposes we restrict attention to groups of projective collineations,** and in order to get a more exact classification of theorems we narrow the Kleinian definition by assigning to the geometry corresponding to a given group only the theory of those properties which, while invariant under this group, are not invariant under any other group of projective collineations containing it.  This will render the question definite as to whether a given theorem belongs to a given geometry.

Perhaps the simplest example of a subgroup of the projective group in a plane is the set of all projective collineations which leave a line of the plane invariant.  The present chapter is concerned chiefly with the geometry belonging to this group." 

* Cf. F. Klein, Vergleichende Betractungen uber neue geometrische Forschungen, Erlangen 1872; also in Mathematische Annalen, Vol. XLIII (1893), p. 63

** From some points of view it would have been desirable to include also all projective groups containing correlations.

The MOG may be regarded as summarizing a geometric structure featuring 759 eight-sets ("octads") in a "space" of 24 points.  The set of 759 octads is left invariant by the transformations of the large Mathieu group M24.  A subgroup, the octad stabilizer, leaves an octad invariant (as a set, though not pointwise).  It so happens that the octad stabilizer, which may be viewed as acting separately on the stabilized octad and on the set of the remaining 16 points of the 24, is isomorphic to the automorphism group of the affine 4-space over the 2-element field.  (In fact, the two parts of this group's action illustrate the isomorphism of the alternating group on eight elements with the general linear group acting on the 4-space over the 2-element field; the stabilized octad is left fixed pointwise by the translations of the affine 4-space.)  A standard theorem of projective geometry says that we may adjoin to an affine n-space an (n-1)-dimensional projective "hyperplane at infinity" to obtain a projective n-space.  The group of the geometry of the affine n-space is the subgroup of the group of the projective n-space leaving the "hyperplane at infinity" invariant (as a set, not pointwise), as in Veblen's discussion above.  One might argue that a stabilized octad in the Mathieu geometry plays a role in some way analogous to that of a "hyperplane at infinity."

Related material:
  1. Chapter 5, "Sporadic Groups," of Finite Simple Groups, by Robert A. Wilson (in preparation as of August 15, 2007).

  2. The Conway-Sloane book has a version of the MOG that differs from the original Curtis MOG by a mirror reflection:

    From Conway and Sloane

    The first edition of the Conway-Sloane book was published in 1988. Conway and Sloane supply a brief discussion of the square structures in the Curtis MOG as pictures of the finite geometry AG(4,2), but make no reference to the work, ten years earlier, of Cullinane.

  3. Steven H. Cullinane, Geometry of the 4x4 Square and The Diamond Theorem.

  4. Thomas M. Thompson, From Error-Correcting Codes through Sphere Packings to Simple Groups. Mathematical Association of America, Washington, 1983.
"While the reader may draw many a moral from our tale,
I hope that the story is of interest for its own sake.
Moreover, I hope that it may inspire others, participants
or observers, to preserve the true and complete record of
our mathematical times."

-- Thomas M. Thompson, op. cit.


Page created Nov. 30, 2005, by Steven H. Cullinane.  Last modified March 6, 2008.