"In this article, we begin a theory linking hyperplane arrangements and invariant forms for reflection groups over arbitrary fields.... Let V  be an n-dimensional vector space over a field F, and let G ≤ Gl_n (F) be a finite group.... An element of finite order in Gl(V ) is a reflection if its fixed point space in V  is a hyperplane, called the reflecting hyperplane. There are two types of reflections: the diagonalizable reflections in Gl(V ) have a single nonidentity eigenvalue which is a root of unity; the nondiagonalizable reflections in Gl(V ) are called transvections and have determinant 1 (note that they can only occur if the characteristic of F is positive).... A reflection group is a finite group G  generated by reflections."

-- Julia Hartmann and Anne V. Shepler, "Reflection Groups and Differential Forms," Mathematical Research Letters, Vol. 14, No. 6 (Nov. 2007), pp. 955-971

"… the class of reflections is larger in some sense over an arbitrary field than over a characteristic zero field. The reflections in Gl(V ) not only include diagonalizable reflections (with a single nonidentity eigenvalue), but also transvections, reflections with determinant 1 which can not be diagonalized. The transvections in Gl(V ) prevent one from developing a theory of reflection groups mirroring that for Coxeter groups or complex reflection groups."

– Julia Hartmann and Anne V. Shepler, "Jacobians of Reflection Groups," Transactions of the American Mathematical Society, Vol. 360, No. 1 (2008), pp. 123-133 (Pdf available at CiteSeer.)

A definition from 1955:

"An invertible linear transformation of a finite dimensional vector space V over a field K will be called a reflection if it is of order two and leaves a hyperplane pointwise fixed. A group G of linear transformations of V is a finite reflection group if it is a finite group generated by reflections." --Claude Chevalley, "Invariants of Finite Groups Generated by Reflections," American Journal of Mathematics, Vol. 77, No. 4 (Oct., 1955), pp. 778-782

This note points out that the above definitions include the simple group of order 168, which is isomorphic to GL(3,2), the general linear group of three dimensions over the two-element field.

We may visualize this group as generated by reflections in the form of certain permutations of parts of the eightfold cube (below) that all fix the same (arbitrarily selected) subcube. 

The eightfold cube

Generating reflections

 

For details, see The Fano Plane Revisualized and Binary Coordinate Systems. For a check of the proof in the latter, see a MAGMA calculation.

There are larger easily-visualized finite reflection groups over the binary field (and, of course, a smaller such group). See Finite Geometry of the Square and Cube.

Update of Feb. 15, 2010-- Background: Coxeter Groups Theorems 15.1 and 15.2 of Alexandre Borovik's book (1st ed. Nov. 10, 2009) Mirrors and Reflections: The Geometry of Finite Reflection Groups– 15.1 (p. 114): Every finite reflection group is a Coxeter group. 15.2 (p. 114): Every finite Coxeter group is isomorphic to a finite reflection group. Consider in this context the above simple reflection group of order 168. (Recall that "…there is only one simple Coxeter group (up to isomorphism); it has order 2…" –A.M. Cohen.) Update of Feb. 18, 2010-- Truth, Geometry, Algebra 1. According to H.S.M. Coxeter and Richard J. Trudeau "There is a pleasantly discursive treatment of Pontius Pilate's unanswered question 'What is truth?'." – Coxeter, 1987, introduction to Trudeau's The Non-Euclidean Revolution 1.1 Trudeau's Diamond Theory of Truth 1.2 Trudeau's Story Theory of Truth 2. According to Alexandre Borovik and Steven H. Cullinane 2.1 Coxeter Theory according to Borovik 2.1.1 The Geometry–           Mirror Systems in Coxeter Theory 2.1.2 The Algebra–           Coxeter Languages in Coxeter Theory 2.2 Diamond Theory according to Cullinane 2.2.1 The Geometry–            Examples: Eightfold Cube and Solomon's Cube 2.2.2 The Algebra–            Examples: Cullinane and (rather indirectly related) Gerhard Grams Summary of the story thus far: Diamond theory and Coxeter theory are to some extent analogous-- both deal with reflection groups and both have a visual (i.e., geometric) side and a verbal (i.e., algebraic) side.  Coxeter theory is of course highly developed on both sides. Diamond theory is, on the geometric side, currently restricted to examples in at most three Euclidean (and six binary) dimensions. On the algebraic side, it is woefully underdeveloped. For material related to the algebraic side, search the Web for generators+relations+"characteristic two" (or "2") and for generators+relations+"GF(2)". (This last search is the source of the Grams reference in 2.2.2 above.) Update of Feb. 21, 2010-- Reflections From the Wikipedia article "Reflection Group" that I created on Aug. 10, 2005– as revised on Nov. 25, 2009– Historically, (Coxeter 1934) proved that every reflection group [Euclidean, by the current Wikipedia definition] is a Coxeter group (i.e., has a presentation where all relations are of the form ri2 or (rirj)k), and indeed this paper introduced the notion of a Coxeter group, while (Coxeter 1935) proved that every finite Coxeter group had a representation as a reflection group [again, Euclidean], and classified finite Coxeter groups. Finite fields This section requires expansion. When working over finite fields, one defines a "reflection" as a map that fixes a hyperplane (otherwise for example there would be no reflections in characteristic 2, as −1=1 so reflections are the identity). Geometrically, this amounts to including shears in a hyperplane. Reflection groups over finite fields of characteristic not 2 were classified in (Zalesskiĭ & Serežkin 1981). 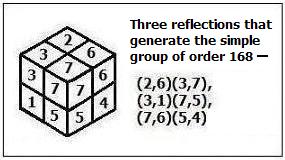Related material: This note, "A Simple Reflection Group of Order 168," and "Determination of the Finite Primitive Reflection Groups over an Arbitrary Field of Characteristic Not 2," by Ascher Wagner, U. of Birmingham, received 27 July 1977 Journal   Geometriae Dedicata Publisher   Springer Netherlands Issue   Volume 9, Number 2 / June, 1980 [A primitive permuation group preserves no nontrivial partition of the set it acts upon.] Clearly the eightfold cube is a counterexample. Update of Feb. 24, 2010-- Transvections A topic related to the above material on reflection groups over GF(2)-- Transvection groups over GF(2). See, for instance... Binary Coordinate Systems, by Steven H. Cullinane, 1984 Classification of the Finite N-Generator Transvection Groups Over Z2, by Jizhu Nan and Jing Zhao, 2009, Advances in Applied Mathematics Vol. 44 Issue 3 (March 2010), 185–202 Anne Shepler, video of a talk on Nov. 4, 2004, "Reflection Groups and Modular Invariant Theory" Update of July 8, 2010-- Coxeter vs. Fano Excerpts from Coxeter's Projective Geometry sketch his attitude toward geometry in characteristic two.

Update of November 27, 2012—