A related image search, for Cremona
synthemes, is omitted here,
but one result from the search is retained...
Note particularly the following image:
This is from Inscapes.
| Finite
Geometry Notes
|
Classical Geometry in Light of Galois Geometry
The following journal notes discuss the relationship of three frontispiece figures from Baker's Principles of Geometry (six volumes, the first four in 1922-1925) to the Galois projective 3-space PG(3,2).
The Rosenhain and Göpel tetrads within PG(3,2) are shown to underlie these figures. The Göpel tetrads underlie the Cremona-Richmond figure that is the frontispiece of Baker's Volume IV (Higher Geometry). The Rosenhain tetrads underlie the figure illustrating Desargues's theorem that is the frontispiece of Baker's Volume I (Foundations).
The Göpel tetrads also underlie Baker's frontispiece illustrating Pascal's Hexagrammum Mysticum in Volume II (Plane Geometry). A Galois-geometry key to the mystic hexagram is taken from a May 26, 1986 note on 2-subsets of a 6-set and PG(3,2).
The 8-sets (and the associated Galois geometry PG(3,2)) in the Miracle Octad Generator (MOG) of R. T. Curtis turn out be closely related to the Hexagrammum via the 354 configuration of Danzer discussed in a recent paper.
The Journal Notes:
Sunday, March 31, 2013 (Easter)
For Pascal
Sunday, March 31, 2013
For Baker
Baker, Principles of Geometry, Vol. IV (1925), Title:
Baker, Principles of Geometry, Vol. IV (1925), Frontispiece:
Baker's Vol. IV frontispiece shows "The Figure of
fifteen
lines
and fifteen points, in space of four dimensions."
Another such figure in a vector space of four
dimensions
over the two-element Galois field GF(2):
(Some background grid parts were blanked by an image resizing process.)
Here the "lines" are actually planes in
the vector 4-space over GF(2),
but as planes through the origin in
that space, they are projective lines
.
For some background, see today's previous post and Inscapes.
Update of 9:15 PM March 31
The following figure relates the above
finite-geometry
inscape incidences to
those in
Baker's frontispiece. Both the inscape
version and that of Baker depict a Cremona-Richmond
configuration.
Monday, April 1, 2013
Desargues via Rosenhain
Background: Rosenhain and Göpel Tetrads in PG(3,2)
Introduction
(an update added on April 19, 2013):
|
The Large Desargues Configuration Desargues' theorem according to a standard textbook: "If two triangles are perspective from a point The converse, from the same book: "If two triangles are perspective from a line Desargues' theorem according
to Wikipedia "Two triangles are in perspective axially [i.e.,
from a line] A figure often used to illustrate the
theorem, A discussion of the "if and only if" version of
the theorem This large Desargues
configuration involves a third triangle, Point-line incidence in this larger configuration
is, The third triangle, within the larger
configuration,
|
A
connection discovered today (April 1, 2013)—
Update of April 18, 2013
Note that
Baker's Desargues-theorem figure has three triangles,
ABC, A'B'C', A"B"C", instead of the two triangles that
occur in
the statement of the theorem. The third triangle appears in the
course of proving,
not just stating, the theorem (or, more precisely,
its converse). See, for instance, a note
on a standard textbook
for
further details.
(End of April 18, 2013 update.)
Update of April 14, 2013
See Baker's
Proof (Edited for the Web) for a detailed explanation
of the above picture of Baker's Desargues-theorem frontispiece.
(End of April 14, 2013 update.)
Update of April 12, 2013
A different figure,
from a site at National
Tsing Hua University,
shows the three triangles of Baker's figure more clearly:
(End of April 12, 2013 update)
Update of April 13, 2013
Another in a series
of figures illustrating
Desargues's theorem in light of Galois geometry:
See also the original Veblen-Young figure in context.
(End of April 13, 2013 update.)
Rota's remarks, while perhaps not completely accurate,
provide
some context
for the above Desargues-Rosenhain connection. For some other
context,
see the interplay in this journal between classical and finite
geometry, i.e.
between Euclid
and Galois.
For the recent context
of the above finite-geometry version of Baker's Vol.
I
frontispiece, see Sunday evening's finite-geometry
version of Baker's Vol.
IV
frontispiece, featuring the Göpel, rather than the Rosenhain, tetrads.
For a 1986 illustration of Göpel and Rosenhain tetrads
(though
not under
those names), see Picturing
the Smallest Projective 3-Space.
In summary... the following
classical-geometry
figures
are closely
related to the Galois geometry PG(3,2):
| Volume I of Baker's Principles has a cover closely related to the Rosenhain tetrads in PG(3,2) |
Volume IV of Baker's Principles has a cover closely related to the Göpel tetrads in PG(3,2) |
| Foundations (click to enlarge)
|
Higher Geometry (click to enlarge)
|
Tuesday, April 2, 2013
The geometry posts of Sunday and Monday have been
placed in finitegeometry.org as
Classical Geometry in Light of Galois Geometry.
Some background:
See Baker, Principles
of Geometry , Vol. II, Note I
(pp. 212-218)—
On Certain Elementary Configurations, and
on the Complete Figure for Pappus's Theorem
and Vol. II, Note II (pp. 219-236)—
On the Hexagrammum Mysticum of Pascal.
Monday's
elucidation of Baker's Desargues-theorem figure
treats the figure as a 154203 configuration
(15 points,
4 lines on each, and 20 lines, 3 points on each).
Such a treatment is by no means new. See Baker's notes
referred to above, and
"The
Complete Pascal Figure Graphically Presented,"
a webpage by J. Chris Fisher and Norma Fuller.
What is new in the Monday Desargues post is the graphic
presentation of Baker's frontispiece figure using Galois
geometry :
specifically, the
diamond theorem square model of PG(3,2).
See also Cremona's kernel, or nocciolo :
Baker on Cremona's approach to Pascal—
"forming, in Cremona's phrase, the nocciolo of the whole."
A related nocciolo :
Click on the nocciolo for
some
geometric background.
Saturday, April 6, 2013
Pascal
via Curtis
Click image for some background.
Shown above is a rearranged version of the
Miracle
Octad Generator (MOG) of R. T. Curtis
("A new combinatorial approach to M24,"
Math. Proc. Camb. Phil. Soc., 79 (1976),
25-42.)
The 8-subcell rectangles in the left part of the figure
may be
viewed as illustrating (if the top left subcell in each is disregarded)
the thirty-five 3-subsets of a 7-set.
Such a view relates, as the remarks below show, the
MOG's underlying Galois geometry, that of
PG(3,2), to
the mystic hexagram of
Pascal.
On Danzer's 354 Configuration:
"Combinatorially, Danzer’s configuration can be
interpreted
as defined by all 3-sets and all 4-sets that can be formed
by the elements of a 7-element set; each 'point' is represented
by one of the 3-sets, and it is incident with those lines
(represented by 4-sets) that contain the 3-set."
– Branko Grünbaum, "Musings
on an Example of Danzer's,"
European Journal of Combinatorics ,
29 (2008),
pp. 1910–1918 (online March 11, 2008)
"Danzer's configuration is deeply rooted in
Pascal's Hexagrammum Mysticum ."
– Marko Boben, Gábor Gévay, and Tomaž Pisanski,
"Danzer's Configuration Revisited," arXiv.org, Jan. 6, 2013
For an approach to such configurations that differs from
those of Grünbaum, Boben, Gévay, and Pisanski, see
Classical Geometry in Light of Galois Geometry.
Grünbaum has written little about Galois geometry.
Pisanski has recently touched on the subject;
see Configurations in
this journal (Feb. 19, 2013).
Sunday, April 7, 2013
Pascal Inscape
Background: Inscapes and The
2-subsets of a 6-set are the points of a PG(3,2).
Tuesday, April 23, 2013
The configurations recently discussed in
"Classical Geometry in Light of Galois Geometry"
are not unrelated to the 27 "Solomon's
Seal Lines"
extensively studied in the 19th century.
See, in particular—
The following figures supply the connection of
Henderson's
six-set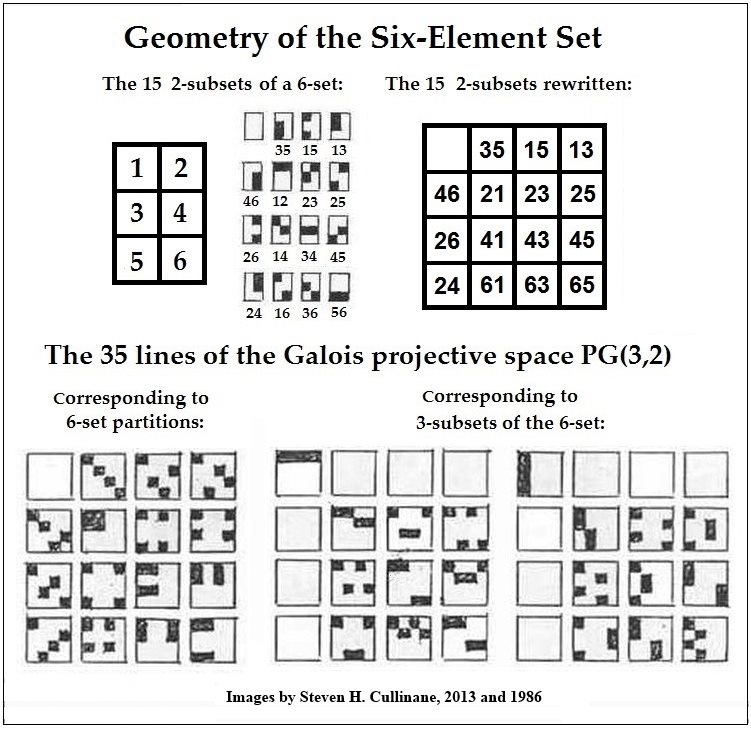
to the Galois geometry previously discussed in "Classical
Geometry…"—
Update of August 16, 2013:
Click above image for some background from 1986.
Related material on six-set geometry from the classical literature—
Baker,
H. F., "Note II: On the Hexagrammum
Mysticum of Pascal,"
in Principles
of Geometry , Vol. II, Camb. U. Press, 1930, pp. 219-236
Richmond,
H. W., "The Figure Formed from Six
Points in Space of Four Dimensions,"
Mathematische Annalen (1900), Volume
53, Issue 1-2, pp 161-176
Richmond,
H. W., "On the Figure of Six Points
in Space of Four Dimensions,"
Quarterly Journal of Pure and Applied
Mathematics , Vol. 31 (1900), pp. 125-160
Page created April 1, 2013.