Annals of Geometry:
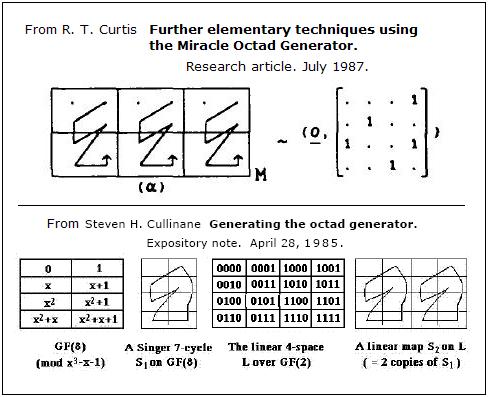
A 1987 article by R. T. Curtis on the geometry of his Miracle Octad Generator (MOG) as it relates to the geometry of the 4x4 square is now available online ($20):
Further elementary techniques using the miracle octad generator, by R. T. Curtis. Abstract:
"In this paper we describe various techniques, some of which are already used by devotees of the art, which relate certain maximal subgroups of the Mathieu group M24, as seen in the MOG, to matrix groups over finite fields. We hope to bring out the wealth of algebraic structure* underlying the device and to enable the reader to move freely between these matrices and permutations. Perhaps the MOG was mis-named as simply an 'octad generator'; in this paper we intend to show that it is in reality a natural diagram of the binary Golay code."
(Received July 20 1987)
(Published online by Cambridge University Press 19 Dec 2008.)
In the above article, Curtis explains how two-thirds of his 4x6 MOG array may be viewed as the 4x4 model of the four-dimensional affine space over GF(2). (His earlier 1974 paper (below) defining the MOG discussed the 4x4 structure in a purely combinatorial, not geometric, way.)
For further details, see The Miracle Octad Generator as well as Geometry of the 4x4 Square and Curtis's original 1974 article, which is now also available online ($20):
A new combinatorial approach to M24, by R. T. Curtis. Abstract:
"In this paper, we define M24 from scratch as the subgroup of S24 preserving a Steiner system S(5, 8, 24). The Steiner system is produced and proved to be unique and the group emerges naturally with many of its properties apparent."
(Received June 15 1974)
-- Mathematical Proceedings of the Cambridge Philosophical Society (1976), 79: 25-42, doi:10.1017/S0305004100052075.(Published online by Cambridge University Press 24 Oct 2008.)
*
For instance:
Click for details.
Click for details.